Composizione cinematica delle rotazioni e degli spostamenti

Prima di affrontare questo argomento, assicurati di aver chiare le nozioni di: componenti assolute di spostamento generalizzato, componenti relative di spostamento generalizzato, deformabilità assiale, deformabilità flessionale, deformabilità tagliante, ipotesi di piccoli spostamenti, principio di sovrapposizione degli effetti.

Generalità

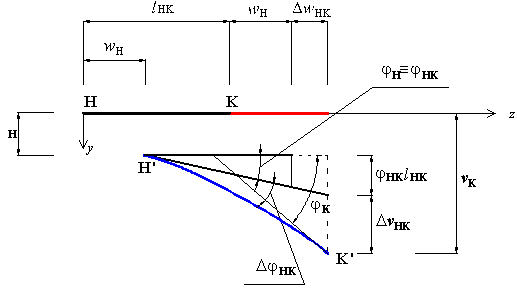
Fig. 1

In riferimento a due generiche sezioni H e K (Fig. 1), le componenti di spostamento generalizzato (traslazione verticale, v, traslazione orizzontale, w, rotazione, j) della sezione K possono essere determinate in funzione delle componenti di spostamento generalizzato della sezione H.

Adottando il sistema di riferimento cartesiano ortogonale estrinseco con origine nell’estremo H, asse z disteso lungo la retta HK e orientato da H verso K, asse y ruotato rispetto all’asse z di un angolo orario di p/2 , le relazioni tra le componenti di spostamento in H (note) e K (incognite), nell'ambito della validità dell'ipotesi di piccoli spostamenti, sono le seguenti (il sistema di riferimento è estrinseco quando la sua posizione non varia con la deformazione del corpo: H si porta in H' ma l'origine del sistema rimane in H):

essendo

v_H lo spostamento assoluto lungo l'asse y della sezione H (positivo se concorde con il verso positivo di y);

l_HK la distanza tra H e K;

Dv_HK lo spostamento relativo lungo y di K rispetto a H, dovuto alla deformazione elastica dell'asta (se si trascura la deformabilità tagliante, tale spostamento relativo elastico è dovuto alla sola deformabilità flessionale) e alle deformazioni per distorsioni termiche a farfalla.

w_H lo spostamento assoluto lungo l'asse z della sezione H (positivo se concorde con il verso positivo di z);

Dw_HK lo spostamento relativo lungo z di K rispetto a H, dovuto alla deformazione elastica (assiale) dell'asta e alle deformazioni per distorsioni termiche uniformi;

j_Hla rotazione assoluta di H;

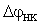la rotazione relativa tra le sezioni H e K, dovuta alla deformazione elastica flessionale e alle deformazioni per distorsioni termiche a farfalla.

Gli spostamenti relativi Dv_HK si intendono positivi se tendono a far aumentare la distanza relativa lungo y di K rispetto a H. Analogamente, gli spostamenti relativi Dw_HK si intendono positivi se tendono a far aumentare la distanza relativa lungo x di K rispetto a H. Le rotazioni relative Dj_HK e assolute j_H si intendono positive se orarie.

Dalla prima relazione, si ricava lo spostamento verticale di K rispetto a H e nella forma:

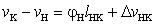
Allo stesso modo, per lo spostamento orizzontale di K rispetto a H e la rotazione relativa tra H e K si ricava:

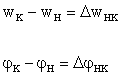
Si osservi come, applicando più volte la composizione cinematica delle rotazioni e degli spostamenti, sia possibile esprimere le componenti di spostamento assoluto di un nodo in funzione delle componenti di spostamento assoluto e relativo dei nodi che precedono. Di conseguenza, è sempre possibile esprimere le componenti di spostamento assoluto cercate in funzione delle componenti di spostamento di un nodo vincolato (note dalle condizioni cinematiche imposte dal vincolo).

Primo esempio

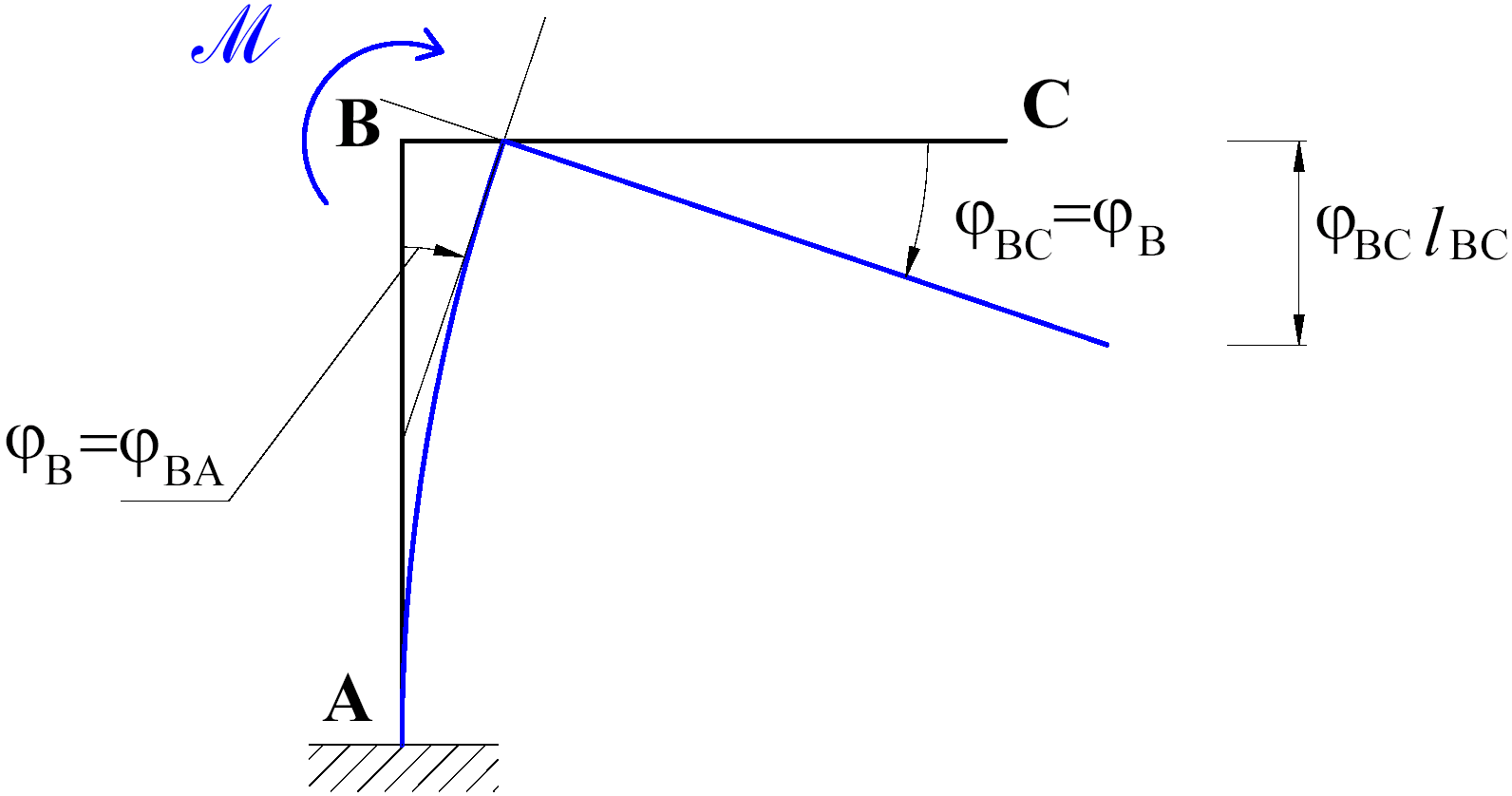
Fig. 2

Per determinare la componente di spostamento assoluto verticale, v_C, del nodo C in Fig. 2, si osservi come il momento flettente M sia identicamente nullo su tutte le sezioni comprese tra B e C. Dunque, anche la curvatura del tronco BC, legata al momento flettente dalla relazione:

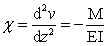è nulla per tutte le sezioni comprese tra B e C. Ne segue che il tronco BC ammette solo componenti di spostamento per atto di moto rigido di rototraslazione, che sono uguali alle componenti di spostamento del nodo B, inteso appartenente al tronco AB. Perciò, è possibile calcolare le componenti di spostamento di C in funzione delle componenti di spostamento assoluto e relativo in B (v_B, j_B, Dv_BC) del tronco AB, che è una mensola incastrata in A e soggetta in B alla coppia esterna .

La rotazione in B del tronco AB, pertanto, si deduce dallo schema elementare a mensola con coppia concentrata all'estremo libero:

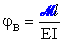
e, per quanto detto, è uguale alla rotazione rigida del tronco BC.

Come mostrato nelle Generalità, lo spostamento verticale di C è somma di tre contributi:

1. Spostamento verticale assoluto di B, v_B. Per la struttura in Fig. 2, v_B è nullo perché, nell'ambito della teoria linearizzata dei piccoli spostamenti, il nodo B della mensola AB si muove lungo una traiettoria che è ortogonale in B alla retta AB. Infatti, se gli spostamenti sono piccoli nel senso della teoria linearizzata, si assume che un'asta non subisca variazione di lunghezza se la proiezione della configurazione deformata sulla configurazione indeformata ha la stessa lunghezza della configurazione indeformata:

2. Spostamento verticale di C causato dalla rotazione rigida in B dell’asta BC, j_B. Tale contributo è pari al prodotto tra la lunghezza del tratto BC e la tangente dell'angolo di rotazione rigida. Poiché, nell'ambito della teoria dei piccoli spostamenti, è possibile confondere la tangente di un angolo con l'angolo stesso, lo spostamento verticale relativo di C rispetto a B si può esprimere come (spostamenti verticali positivi se diretti verso il basso):

con j_B dedotto dallo schema elementare a mensola con coppia concentrata all'estremo libero.

3. Spostamento verticale relativo tra gli estremi B e C dovuto alla deformazione elastica dell’asta. Come osservato in precedenza, per la particolare condizione di carico considerata il tronco BC non ammette componenti di spostamento per deformabilità elastica. Pertanto:

Per composizione cinematica delle rotazioni e degli spostamenti, la somma dei tre contributi fornisce:

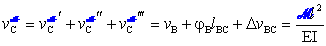Secondo esempio

Anche nel caso della struttura in Fig. 3, lo spostamento verticale assoluto in C, v_C, può essere calcolato in funzione delle componenti di spostamento assoluto e relativo del nodo che precede il nodo C, il nodo B (v_B, j_B, Dv_BC):

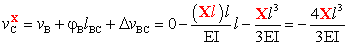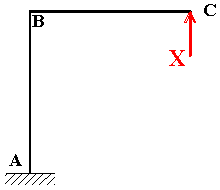
Fig. 3

dove la rotazione assoluta j_B è stata calcolata in funzione delle componenti di spostamento assoluto e relativo del nodo che precede il nodo B, il nodo A (v_A, Dj_AB):

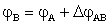
ricordando che, per le condizioni cinematiche del vincolo in A (incastro perfetto), deve essere j_A = 0.

Per il calcolo di Dj_AB, invece, ci si è ricondotti alla rotazione dell’estremo libero dello schema elementare a mensola in Fig. 4.A, sollecitato dalle azioni X e Xl trasmesse al nodo B dalla porzione di struttura soppressa (tronco BC). Ne segue:

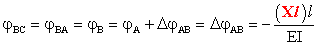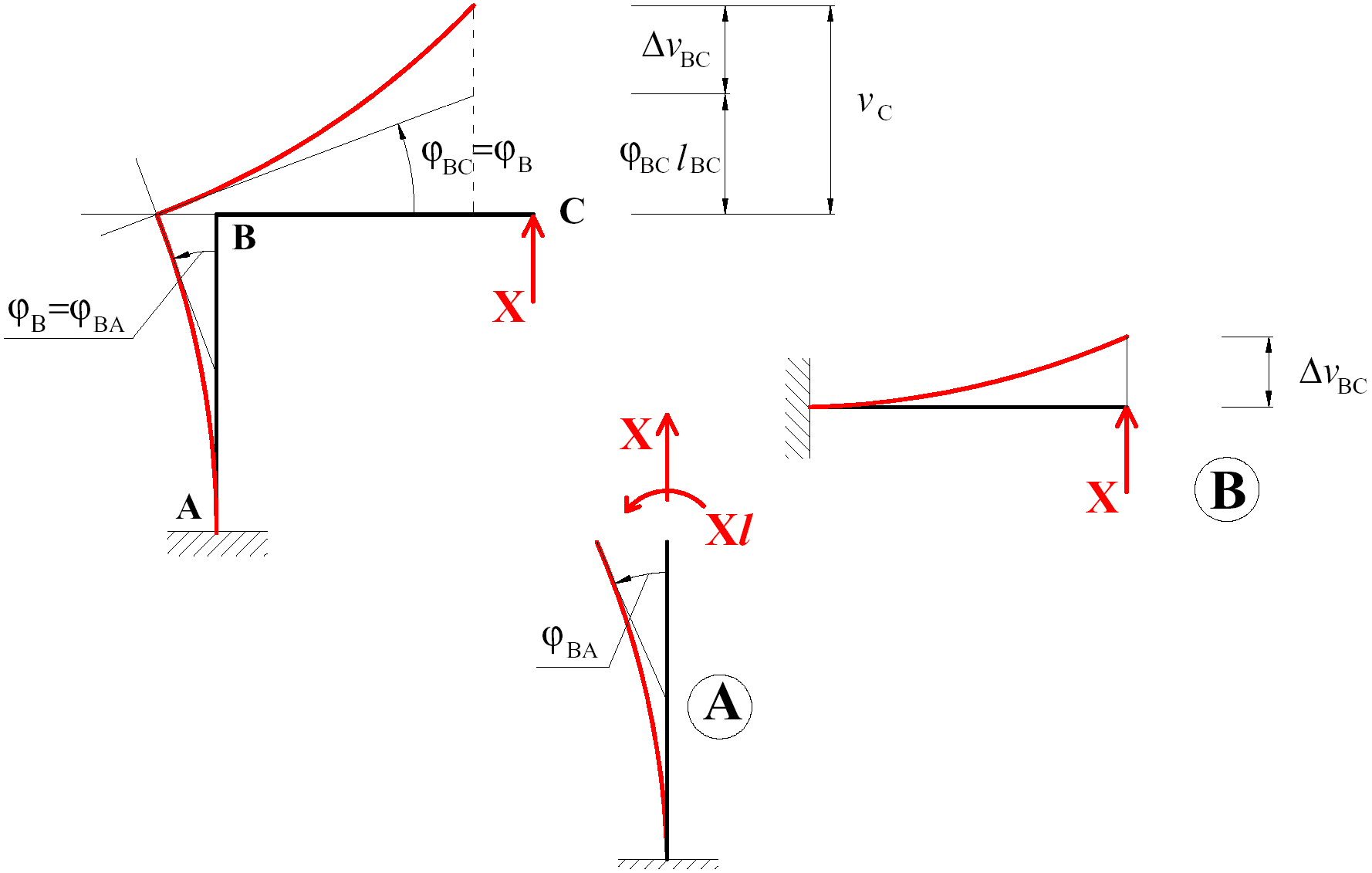
Fig. 4

In alternativa, per valutare lo spostamento in C causato dalla forza concentrata X si può pensare di aggiungere nel nodo B un sistema autoequilibrato di forze, come mostrato in Fig. 5.

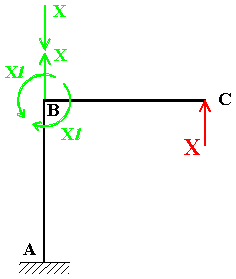
Fig. 5

Per il principio di sovrapposizione degli effetti, è possibile suddividere il sistema di forze in Fig. 5 in due sottoinsiemi complementari di forze, studiare il telaio ABC caricato, la prima volta, dal primo sottoinsieme di forze e, la seconda volta, dal secondo sottoinsieme di forze e, infine, calcolare lo spostamento verticale in C sommando gli spostamenti in C conseguenti ai due sottoinsiemi, studiati separatamente.

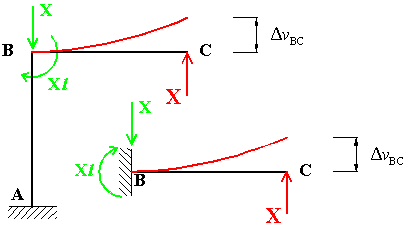
Fig. 6

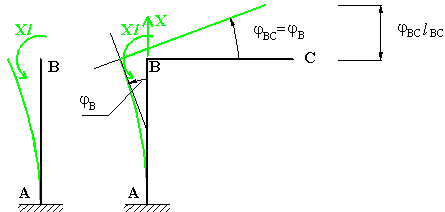
Fig. 7

Scegliendo di suddividere il sistema di forze in Fig. 5 nei due sottoinsiemi complementari mostrati in Fig. 6 e 7, Il tronco BC in Fig. 6 si comporta come una mensola incastrata in B. Infatti la forza e la coppia applicate in B sono uguali alle reazioni di incastro di una mensola BC con forza concentrata X all'estremo libero C. Dunque, lo spostamento verticale assoluto di C per il sottoinsieme di forze in Fig. 6, uguale allo spostamento verticale relativo di C rispetto a B per deformazione elastica, risulta uguale a (spostamenti verticali positivi se diretti verso il basso):

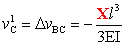Il tronco AB in Fig. 7 è una mensola incastrata in A, sollecitata da una coppia (Xl) e da una forza (X) concentrate. Se si trascura la deformabilità assiale di AB, X non produce alcuna deformazione elastica. Dunque, il nodo B si sposta per effetto della sola coppia Xl, che flette il tronco AB con curvatura costante (essendo costante il momento flettente tra le sezioni A e B).

La rotazione rigida di BC è uguale alla rotazione in B della mensola AB con coppia concentrata Xl all'estremo libero:

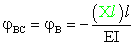Tale rotazione imprime in C un ulteriore spostamento verticale verso l'alto:

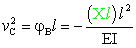In conclusione, per valutare lo spostamento verticale in C causato dalla forza concentrata X:

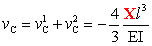si può procedere per fasi successive. In fase 1 si valuta lo spostamento verticale di C sullo schema che si ottiene bloccando fittiziamente la rotazione e lo spostamento di B per mezzo di un incastro in B (vincolo ausiliario). In fase 2 si valuta l'ulteriore componente di spostamento verticale in C sullo schema che si ottiene applicando in B le reazioni vincolari dell'incastro fittizio di Fase 1 (reazioni d'incastro perfetto) cambiate di segno. Questo modo di procedere prende il nome di metodo dei vincoli ausiliari.

Test di verifica dell'apprendimento: