Una omotetia è una particolare trasformazione geometrica del piano o dello spazio, che dilata o contrae gli oggetti, mantenendone la forma e l'orientazione. Si dice omotetia di centro A e rapporto k una trasformazione dello spazio euclideo che "dilata" le distanze da A di tutti i punti secondo un fattore k, non nullo. Ad ogni punto P del piano corrisponde il punto P', allineato con A ed P, tale che AP'/AP = k. L'unico punto che corrisponde a se stesso, e che per questo si dice unito, è il centro A.

    Quando il rapporto di omotetia k è positivo, l'omotetia si dice diretta. In questo caso, il generico punto P viene spostato lungo il semiasse positivo della semiretta uscente dal centro e passante per P, in modo che la sua distanza dal centro cambi secondo il fattore costante k. Questa trasformazione geometrica è anche chiamata dilatazione, se k > 1, contrazione se k < 1. Se k = 1 si ottiene l'identità, ovvero, la trasformazione nella quale ogni punto corrisponde a se stesso.

Omotetia diretta di centro O e rapporto k = 2 della figura ABCD.

    Quando il rapporto di omotetia k è negativo, l'omotetia si dice inversa. In questo caso, il punto P viene spostato lungo il semiasse negativo della semiretta uscente dal centro e passante per P, nel punto che dista dal centro di una quantità pari alla distanza di P dal centro moltiplicata per |k|. L'omotetia di fattore -1 è la simmetria centrale, che coincide con la rotazione di un angolo piatto attorno al centro.

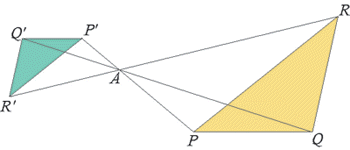
Omotetia inversa di centro A e rapporto k = -1/2 della figura PQR.

Argomenti correlati: