|
ALGEBRA VETTORIALE
1) Vettore. 2) Vettori equipollenti. 3) Vettore applicato. 4) Cursore. 5) Prodotto scalare. 6) Prodotto vettoriale. 7) Vettore somma. 8) Vettore differenza. 9) Momento polare di un vettore e di un sistema di vettori. 10) Coppia. 11) Vettore risultante. 12) Sistemi equivalenti di vettori. 13) Sistemi in equilibrio di vettori. 14) Equazioni cardinali della Statica. 15) Equilibrante di un sistema di vettori 16) Operazioni invariantive. 17) Forza. 18) Risultante di un sistema piano di forze. 19) Sistemi equivalenti di forze. 20) Sistemi in equilibrio di forze. 21) Condizioni di equivalenza a zero. 22) Composizione delle forze nel piano.
GEOMETRIA DELLE MASSE
1) Momento statico. 2) Determinazione grafica ed analitica del baricentro di un sistema continuo di masse. 3) Momenti d’inerzia assiali. 4) Proprietà distributiva dei momenti statici e d’inerzia. 5) Momento d’inerzia polare. 6) Calcolo dei momenti statici d’inerzia e centrifughi delle figure elementari (rettangolo, cerchio, triangolo rettangolo, semicerchio). 7) Utilizzo del momento d’inerzia polare per il calcolo del momento d’inerzia di un cerchio rispetto ad un suo diametro. 8) Primo e terzo teorema del trasporto con applicazioni. 9) Leggi di trasformazione per rotazione del sistema di riferimento; momenti d’inerzia nel sistema di riferimento ruotato; equazioni parametriche in 2a
dei momenti d’inerzia assiali e relativa rappresentazione grafica. 10) Circoli di Mohr: costruzione, momenti principali d’inerzia, polo di Mohr e dimostrazione della sua proprietà fondamentale, assi principali d’inerzia. 11) Procedimento analitico per il calcolo dei momenti e degli assi principali d’inerzia; angoli
a0 per per i quali si ha un estremante di
Ix e valori assunti in loro corrispondenza da
Ixy e Iy, relazione intercorrente tra le derivate seconde di
Ix e Iy. 12) Espressioni dei momenti principali d’inerzia per
Ix0Iy0 e
Ix0 Iy0 e loro interpretazione geometrica. 13) Confronto tra le circonferenze descritte dalle eq. 30 e dalle eq. 38. 14) Raggi d’inerzia; ellisse centrale d’inerzia; equazione segmentaria della retta polare di un punto rispetto all’ellisse centrale d’inerzia; polarità. 15) Poli coniugati in una polarità; rette coniugate in una polarità; teorema di reciprocità per centri propri e impropri. 16) Diametro coniugato alla direzione di una retta e sua costruzione grafica. 17) Antipolo, antipolare, antipolarità, antipoli coniugati nell’antipolarità e loro relazione analitica. 18) Costruzione grafica dell’antipolo e dell’antipolare di un polo assegnato; casi particolari per polo coincidente col baricentro e polo improprio. 19) Nocciolo centrale d’inerzia e sue proprietà.
ANALISI DELLA DEFORMAZIONE
1) Campo di spostamento e sue proprietà. Dilatazione lineare specifica e scorrimento angolare. 2) Linearizzazione del campo di spostamento; affinità; decomposizione del campo di spostamento e suo significato nell’ipotesi di piccoli gradienti di spostamento. 3) Significato fisico della dilatazione lineare specifica e sua rappresentazione grafica. 4) Significato fisico dello scorrimento angolare e sua rappresentazione grafica. 5) Componenti della deformazione pura al ruotare della terna di riferimento; tensore di deformazione infinitesima; vettore algebrico delle componenti di deformazione; operatore di congruenza; sistema di spostamenti-deformazioni cinematicamente ammissibile. 6) Invarianza delle forme bilineari e quadratiche per roto-traslazione della terna di riferimento e conseguenze sui parametri fisici della deformazione. 7) Dimostrazione delle proprietà tensoriali della matrice di deformazione infinitesima a partire dalle componenti di spostamento per i punti dell’intorno infinitesimo di raggio unitario. 8) Proprietà di reciprocità degli spostamenti e sue conseguenze sulla simmetria del tensore di deformazione infinitesima. 9) Componenti principali ed invarianti di deformazione; direzioni principali di deformazione. 10) Ortogonalità delle direzioni principali di deformazione; tensore di deformazione infinitesima ed invarianti di deformazione nel riferimento principale; deformazione di un parallelepipedo retto con le facce ortogonali alle direzioni principali. 11) Coefficiente di dilatazione cubica; tensore volumetrico; deviatore di deformazione. 12) Stati monoassiali e biassiali di deformazione con dimostrazione della condizione necessaria e sufficiente per lo stato piano.
TEORIA DELLA TENSIONE
1) Forze in un solido; equilibrio del corpo libero deformato e indeformato. 2) Vettore tensione; componenti cartesiane e componenti speciali di tensione. 3) Matrice di trasformazione tra componenti speciali e cartesiane di tensione; riferimenti locali sulle facce del cubetto con spigoli paralleli agli assi. 4) Equazioni di Cauchy; simmetria della matrice delle componenti speciali di tensione delle giaciture dei piani coordinati. 5) Teorema di reciprocità delle componenti di tensione e suo corollario. 6) Componenti speciali di tensione al ruotare della terna di riferimento; tensore degli sforzi; vettore algebrico delle componenti di tensione. 7) Invarianza delle forme bilineari e quadratiche per roto-traslazione della terna di riferimento; intorno sferico di raggio unitario. 8) Componenti principali ed invarianti di tensione; giaciture e direzioni principali di tensione. 9) Ortogonalità delle direzioni principali di tensione; tensore degli sforzi ed invarianti di tensione nel riferimento principale. 10) Corrispondenza tra punti della superficie dell’intorno sferico di raggio unitario e punti del piano di Mohr; arbelo di Mohr. 11) Tensione media e suo legame con il primo invariante di tensione; tensore idrostatico e deviatore degli sforzi: definizioni, invarianti, circoli di Mohr, tensioni e direzioni principali. 12) Stati monoassiali e biassiali di tensione con dimostrazione della condizione necessaria e sufficiente per lo stato piano. 13) Stato piano di tensione: circoli di Mohr; proprietà fondamentale del polo di Mohr; metodo delle parallele alle tracce delle giaciture; tensioni, direzioni, assi e tracce delle giaciture principali di tensione per via grafica. 14) Equazioni indefinite di equilibrio e equazioni al contorno per il solido tridimensionale (notazione scalare, notazione matriciale estesa e compatta); operatore di equilibrio; campo di tensioni staticamente ammissibile.
IDENTITÀ FONDAMENTALE E PRINCIPI NELLA MECCANICA DEI SOLIDI
1) Identità integrale fondamentale nella meccanica dei solidi: Teorema e Principio dei Lavori Virtuali per corpi deformabili; Principio dei Lavori Virtuali per corpi rigidi. 2) Variazione; funzione varata; lavoro di deformazione esterno ed interno e sue variazioni; processo di carico quasi statico; lavoro complementare di deformazione.
SISTEMI ELASTICI
1) Spazio delle configurazioni; corpo in stato elastico; densità di energia elastica; energia elastica; densità del potenziale elastico; densità di energia complementare elastica; energia complementare elastica. 2) Stato elastico: sviluppo in serie della densità di energia elastica e delle componenti di tensione; materiali omogenei e non omogenei; ipotesi di piccola deformazione, stato naturale indeformato e autotensioni nulle; costanti elastiche. 3) Forme quadratiche del potenziale elastico e del potenziale elastico complementare; minimo del potenziale elastico. 4) Materiali isotropi e anisotropi; stato elastico lineare per materiali isotropi; leggi generalizzate di Hooke; rapporto tra direzioni principali di tensione e direzioni principali di deformazione. 5) Significato fisico di
E,
n e
G. 6) Problemi dell’equilibrio elastico lineare, dell’equilibrio elastico lineare omogeneo e dell’equilibrio elastico lineare omogeneo isotropo; principi di sovrapposizione degli effetti e di Kirchhoff.
PROBLEMA DI DE SAINT-VENANT
1) Solido di De Saint-Venant: modello geometrico, modello delle azioni esterne e modello reologico, problema di De Saint-Venant e sue equazioni. 2) Postulato di Boussinesq; postulato di De Saint Venant e sue conseguenze. 3) Conseguenza del principio di Kirchhoff; ipotesi di De Saint-Venant e sue conseguenze. 4) Relazioni di equivalenza statica; condizioni integrali ai limiti; quattro casi fondamentali; vettore tensione tangenziale totale per i punti della superficie laterale. 5) Sforzo normale centrato: condizioni ai limiti integrali; ipotesi di lavoro; soluzione del problema; tensore degli sforzi; verifica dell’ipotesi di lavoro. 6) Sforzo normale centrato: campo di spostamento; significato associato all’annullamento delle componenti di moto rigido; deformata della sezione retta. 7) Sforzo normale centrato: circoli di Mohr, giaciture a massima tensione tangenziale, relazione tra direzioni principali di tensione e di deformazione, variazione specifica di volume, casi in cui la soluzione risulta esatta anche all’interno della zona di estinzione, diagramma delle tensioni normali. 8) Flessione retta: condizioni ai limiti integrali, ipotesi di lavoro, soluzione del problema, tensore degli sforzi, verifica dell’ipotesi di lavoro. 9) Flessione retta: campo di spostamento, deformata dell’asse, deformata della sezione retta, significato associato all’annullamento degli scorrimenti angolari, rotazione relativa tra le facce del concio infinitesimo. 10) Flessione retta: dilatazioni lineari specifiche sul piano di sezione, piano e asse neutro, diagramma delle tensioni normali, relazione tra asse neutro e asse vettore momento. 11) Flessione deviata: soluzione per sovrapposizione degli effetti, rotazione dell’asse neutro rispetto all’asse vettore momento per via analitica e per via geometrica (tramite l’asse di sollecitazione): caso generale e casi particolari di asse vettore momento parallelo ad una direzione principale d’inerzia e ellisse centrale d’inerzia di forma circolare, diagramma delle tensioni normali. 12) Sforzo normale eccentrico: centro di pressione, tenso-flessione e presso-flessione, soluzione per sovrapposizione degli effetti, formula trinomia in termini di raggi d’inerzia, equazione dell’asse neutro in forma segmentaria, relazione geometrica tra asse neutro e centro di pressione. 13) Sforzo normale eccentrico: diagrammi delle tensioni normali per tenso- e presso-flessione retta con centro di pressione esterno e interno al nocciolo centrale d’inerzia, rotazione dell’asse neutro rispetto all’asse vettore momento, costruzioni grafiche dell’asse neutro per il caso generale. 14) Torsione: solidi a sezione sottile chiusa e aperta (andamento delle tensioni, fattore di rigidezza torsionale, angolo unitario di torsione), analogia idrodinamica, concentrazioni e cadute di tensione nelle sezioni sottili e compatte. 15) Torsione: circoli di Mohr, isostatiche di trazione e compressione. 16) Taglio retto e flessione: centro di taglio, trattazione approssimata di Jourawski. 17) Taglio retto e flessione: taglio secondo un asse di simmetria (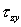 , ,
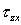 e e
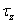 ). ).
VERIFICHE DI RESISTENZA
1) Tensione ideale secondo i criteri di Von Mises e Tresca per stati tensionali alla De Saint-Venant. 2) Verifica a sforzo normale centrato. 3) Verifica a flessione retta ed a flessione deviata. 4) Verifica a sforzo normale eccentrico. 5) Verifica a taglio e flessione. 6) Verifica a taglio e torsione.
MECCANICA DEI MATERIALI
1) Prove di resistenza meccanica in controllo di carico ed in controllo di spostamento. 2) Prove monoassiali di compressione e trazione su materiali fragili: limiti di validità della soluzione di De Saint Venant per sforzo normale centrato, tensore degli sforzi, legami N/v e
s/e, softening, circoli di Mohr, piani di scorrimento nei provini cubici. 3) Prove triassiali di compressione su materiali fragili: legami
s/e e dipendenza dalla pressione di confinamento, tensore degli sforzi, circoli di Mohr, stress path, dominio di crisi nel piano di Mohr, piani di scorrimento nei provini cubici. 4) Circoli di Mohr per lo stato tensionale tangenziale puro; piani di scorrimento; lesioni tipiche degli edifici soggetti a sisma. 5) Piani di scorrimento nei materiali fragili soggetti a trazione monoassiale. 6) Transizione fragile-duttile. 7) Criterio di crisi di Mohr/Coulomb; coesione; angolo di attrito interno; materiali incoerenti. 8) Sensibilità del fattore di sicurezza dei materiali fragili alla pressione di confinamento, benefici della pressione idrostatica sulla resistenza delle murature. 9) Effetto dell’acqua sui circoli di Mohr dei materiali granulari, tensione efficace. 10) Dipendenza della curva
s/e dalla velocità di deformazione; curva limite inferiore e curva limite superiore; viscosità; creep primario, secondario e terziario. 11) Prova di trazione e compressione monoassiale su barre di acciaio: tensore degli sforzi; strizione; legami N/v e
s/e; comportamento allo scarico; incrudimento; softening; legame di Prandtl; tensione ammissibile; tensore di deformazione. 12) Insensibilità del criterio di crisi dei materiali duttili alla pressione di confinamento; criterio di crisi di Tresca.
TEORIA DELLE STRUTTURE
1) Coordinate lagrangiane. 2) Vincoli; molteplicità di vincolo; molteplicità di svincolamento interno; strutture labili; isostatiche ed iperstatiche. 3) Vincoli ben posti e mal posti; dualità statica-cinematica; reazioni vincolari del corpo isostatico per via analitica e per via grafica; curva delle pressioni. 4) Equazioni cardinali della statica per il corpo rigido vincolato; equazioni ausiliarie. 5) Equazioni indefinite d’equilibrio per il solido trave. 6) Caratteristiche della sollecitazione interna per travi spaziali e travi piane. 7) Convenzioni sul tracciamento dei diagrammi di N, M e T nelle travi piane; convenzioni del concio e della punteggiata. 8) Uso delle scale nel tracciamento dei diagrammi dell’azione interna. 9) Nodo triplo. 10) Calcolo delle componenti di reazione esterna ed interna nelle strutture isostatiche chiuse. 11) Strutture reticolari piane; metodo dei nodi; metodo delle sezioni di Ritter. 12) Applicazione del Principio dei Lavori Virtuali ai corpi rigidi per il calcolo delle reazioni vincolari in un sistema staticamente determinato soggetto a forze. 13) Procedimento delle catene cinematiche. 14) Calcolo delle componenti di spostamento nelle strutture isostatiche attraverso il Principio dei Lavori Virtuali. 15) Equazione differenziale della linea elastica. 16) Disegno della configurazione deformata per un sistema di travi. 17) Calcolo delle componenti di spostamento per deformabilità flessionale mediante integrazione dell’equazione differenziale della linea elastica. 18) Composizione cinematica delle rotazioni e degli spostamenti. 19) Simmetria ed emisimmetria strutturale e di carico. 20) Metodo delle forze. 21) Telai a nodi fissi e a nodi spostabili; metodo dei telai a nodi spostabili. 22) Distorsioni di Volterra. 23) Distorsioni termiche uniformi e a farfalla; deformata delle strutture iperstatiche soggette a distorsione termica a farfalla. 24) Cedimenti vincolari elastici e anelastici, rigidezza e cedibilità alla traslazione ed alla rotazione. 25) Espressione generale del Principio dei Lavori Virtuali per i sistemi monodimensionali piani in stato elastico lineare; lavoro virtuale interno nelle strutture reticolari piane. 26) Calcolo delle incognite iperstatiche attraverso il Principio dei Lavori Virtuali.
Testi consigliati:
-
A. DI TOMMASO, FONDAMENTI DI SCIENZA
DELLE COSTRUZIONI, PARTE I, 1981; PARTE
II, 1993, PATRON ED., BOLOGNA
-
E. VIOLA, ESERCITAZIONI DI SCIENZA DELLE
COSTRUZIONI, 1/ STRUTTURE ISOSTATICHE E
GEOMETRIA DELLE MASSE, 2/ STRUTTURE
IPERSTATICHE E VERIFICHE DI RESISTENZA,
PITAGORA ED., BOLOGNA, 1993
-
MATERIALE FORNITO DAL DOCENTE IN FORMA
DI DISPENSA
|