I circoli di Mohr per lo stato piano di tensione

I circoli di Mohr per lo stato piano di tensione (test 2)

Prima di affrontare questo test, assicurati di aver chiare le nozioni di: centro di una stella di piani, circoli di Mohr per lo stato triassiale di tensione, componenti speciali di tensione, fascio di piani, giacitura, omotetia, proprietà del polo di Mohr per lo stato di tensione, sostegno di un fascio di piani, stella di piani, stato piano di tensione, stato triassiale di tensione, tensione normale, tensione tangenziale totale, traccia di un piano.

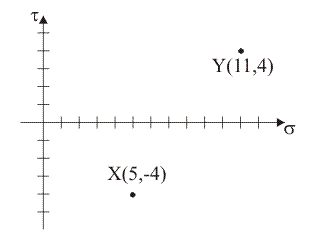
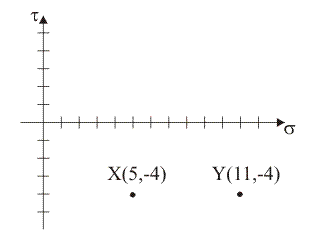
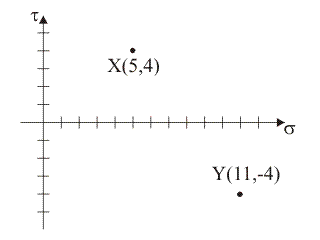
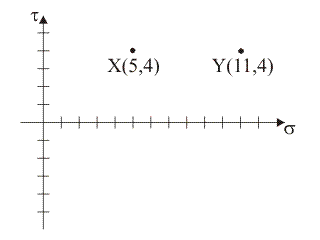
1) Quali punti X e Y del piano di Mohr sono i punti tensione rappresentativi delle componenti normale e tangenziale totale di tensione sulle giaciture di normale x e y?	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
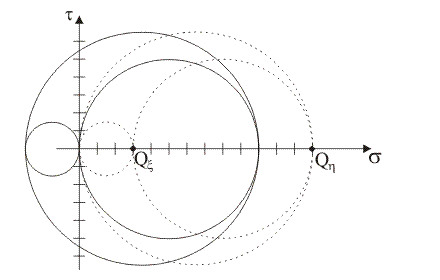
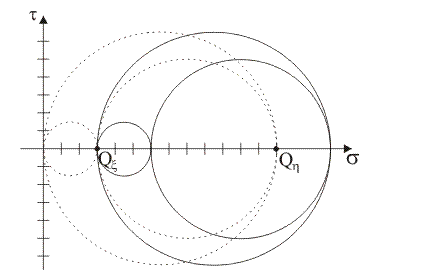
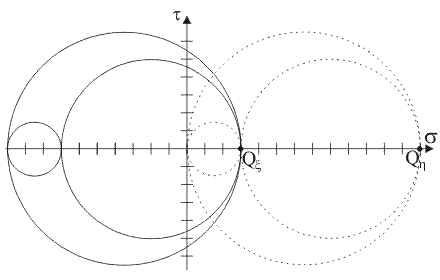
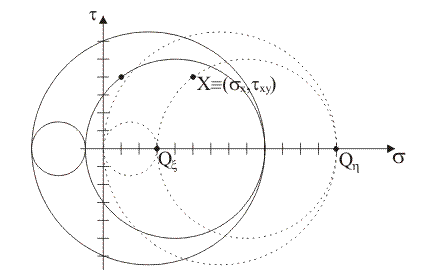
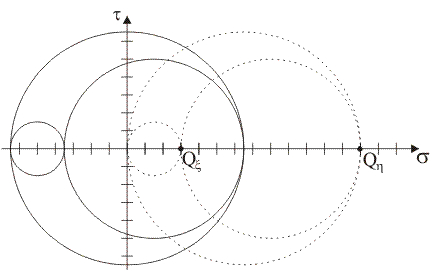
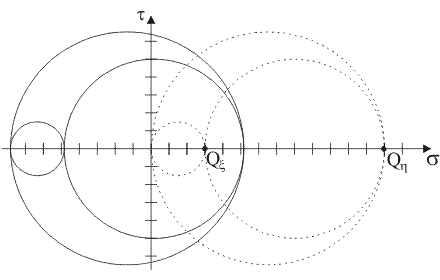
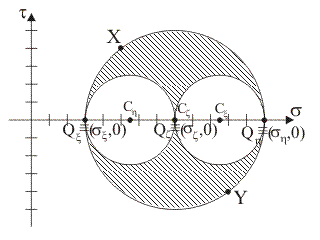
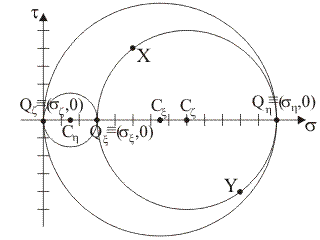
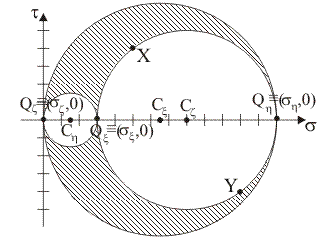
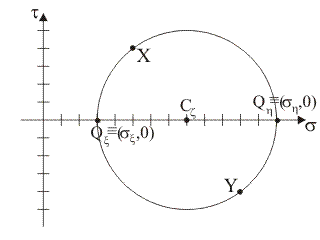
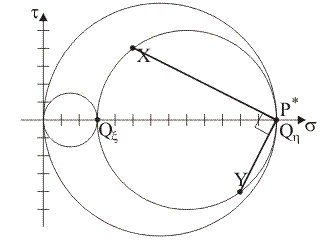
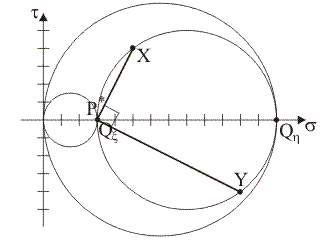
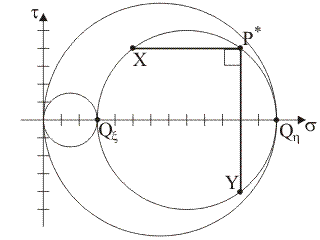
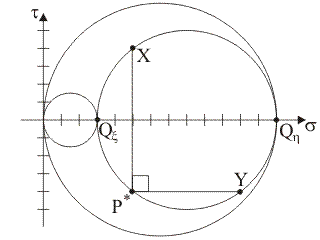
2) Supponendo che i punti tensione del piano di Mohr rappresentativi delle componenti normale e tangenziale totale di tensione sulle giaciture di normale x e y siano, rispettivamente, i punti X≡(5, 4) e Y≡(11, –4), quale tra le seguenti figure rappresenta il luogo delle componenti di tensione sulle giaciture della stella di piani di centro B?	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
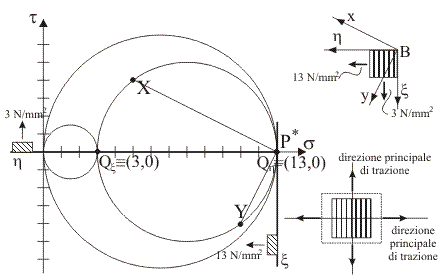
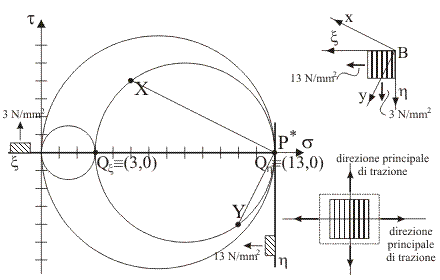
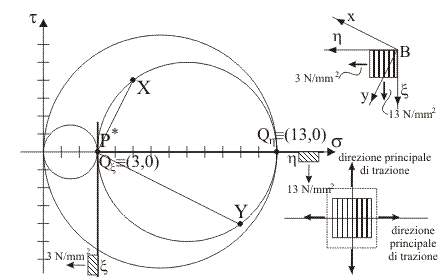
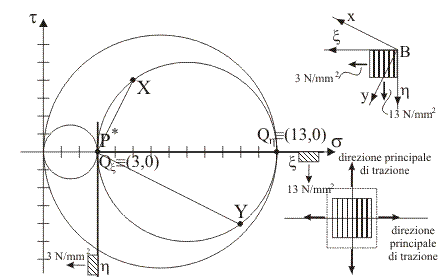
3) Supponendo che i punti tensione del piano di Mohr rappresentativi delle componenti normale e tangenziale totale di tensione sulle giaciture di normale x e y siano, rispettivamente, i punti X≡(5, 4) e Y≡(11, –4), quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione del polo di Mohr, P*, per le giaciture che fanno fascio attorno all'asse z?	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
4) Indicare quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione delle direzioni principali di tensione nel piano x/y tramite il polo di Mohr e quali sono la configurazione indeformata e la configurazione deformata dell'elemento di materia le cui facce sono ortogonali alle direzioni trovate. 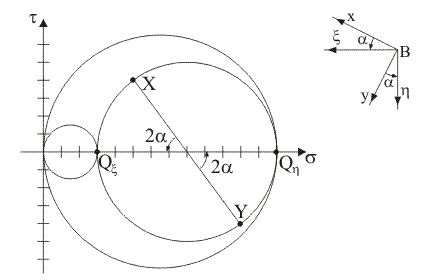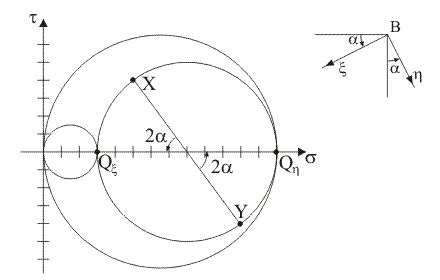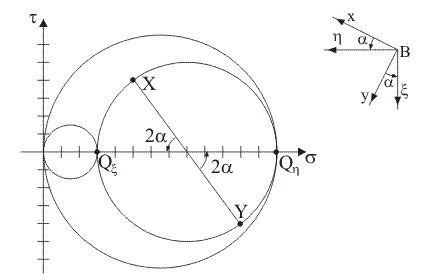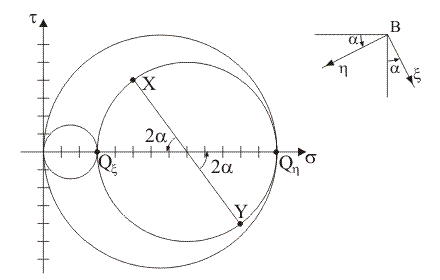x: direzione principale di trazione h: direzione principale di trazione x: direzione principale di trazione h: direzione principale di trazione x: direzione principale di trazione h: direzione principale di trazione x: direzione principale di trazione h: direzione principale di trazione	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
5) Quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione delle direzioni principali di tensione nel piano x/y tramite la corrispondenza tra angoli di rotazione al centro nel piano di Mohr e angoli di rotazione del sistema di riferimento Bxy?	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
6) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del circolo di Mohr che passa per X e Y? L'asse x. L'asse y. L'asse z. L'asse h.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
7) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più piccolo tra i circoli di Mohr che passano per l'origine degli assi? L'asse x. L'asse y. L'asse h. L'asse x.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
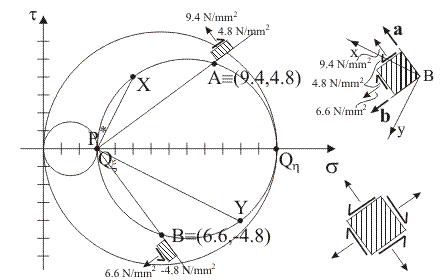
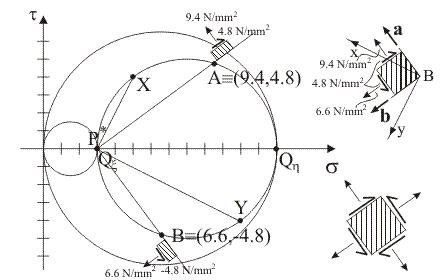
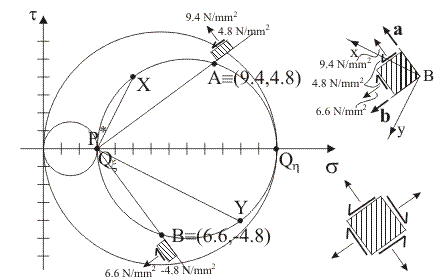
8) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più grande tra i circoli di Mohr che passano per l'origine degli assi? L'asse x. L'asse y. L'asse x. L'asse h.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
9) Indicare i punti tensione rappresentativi della componente normale e della componente tangenziale totale di tensione sulle giaciture di versori normali e 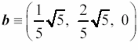, facendo uso del polo di Mohr, e rappresentare il corrispondente stato tensionale nel sistema di riferimento di centro B.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
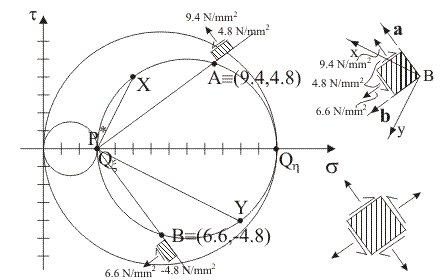
10) Quale tra le seguenti affermazioni è vera? Le giaciture della stella di piani di centro B sulle quali è massima la componente tangenziale totale di tensione appartengono al fascio di piani di sostegno z; le loro tracce sul piano x/y sono rette inclinate di ±45° rispetto agli assi x e y. Le giaciture della stella di piani di centro B sulle quali è massima la componente tangenziale totale di tensione appartengono al fascio di piani di sostegno z; le loro tracce sul piano x/y sono rette inclinate di ±45° rispetto alla direzione orizzontale. Le giaciture della stella di piani di centro B sulle quali è massima la componente tangenziale totale di tensione non appartengono al fascio di piani di sostegno z, ma al fascio di piani di sostegno h; le loro tracce sul piano x/y coincidono con l'asse h, mentre, sul piano x/z, sono rette inclinate di ±45° rispetto alla direzione orizzontale. Le giaciture della stella di piani di centro B sulle quali è massima la componente tangenziale totale di tensione non appartengono al fascio di piani di sostegno z, ma al fascio di piani di sostegno x; le loro tracce sul piano x/y coincidono con l'asse x, mentre, sul piano h/z, sono rette inclinate di ±45° rispetto alla direzione orizzontale.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
11) Quante sono le direzioni principali di tensione per uno stato tensionale idrostatico? Una. Due. Nessuna. Infinite.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
12) Come si deforma l'intorno materiale di centro B soggetto ad uno stato tensionale idrostatico? Non si deforma. Degenera in un punto. Subisce una deformazione omotetica. Le due coppie di piani paralleli che sono ortogonali alle direzioni principali di tensione subiscono una traslazione, le altre coppie di piani subiscono una rotazione.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
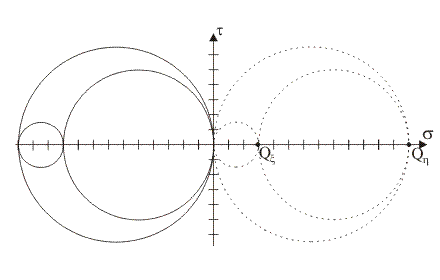
13) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché lo stato tensionale nell'intorno di B sia ancora piano, ma con piano delle tensioni h/z? s_I = –s_x s_I = s_x s_I = –s_h s_I = s_h	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
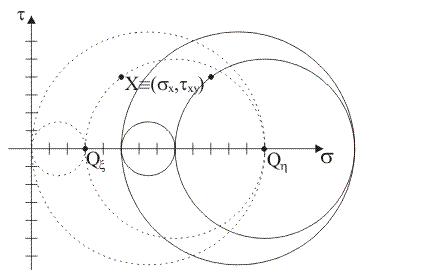
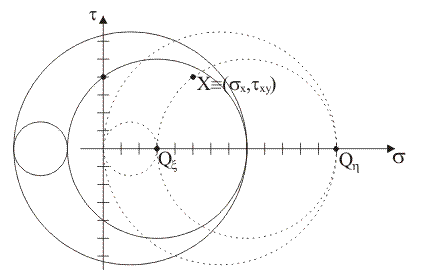
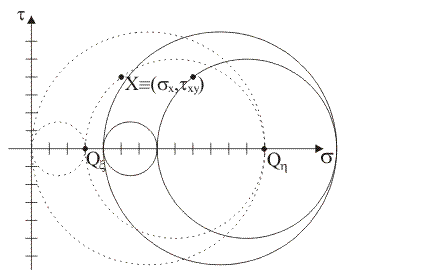
14) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché sulla giacitura di normale x si abbia tensione normale nulla? s_I = s_x s_I = –s_x s_I = t_xy s_I = –t_xy	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
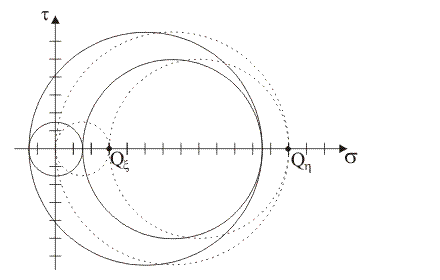
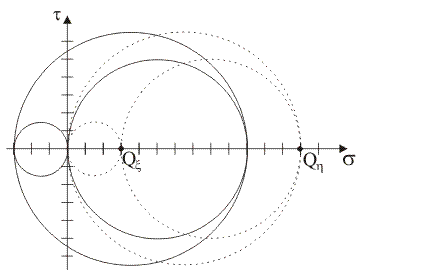
15) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché sulla giacitura per la quale si ha il massimo della tensione tangenziale totale sia nulla la tensione normale? s_I = – 1/2 (s_z + s_h) s_I = – s_x – 1/2 (s_x + s_h) s_I = – 1/2 (s_z + s_x) s_I = – s_x	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
	Punteggio ottenuto: / 30

I circoli di Mohr per lo stato piano di tensione (test 2)

1) Quali punti X e Y del piano di Mohr sono i punti tensione rappresentativi delle componenti normale e tangenziale totale di tensione sulle giaciture di normale x e y?

5) Quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione delle direzioni principali di tensione nel piano x/y tramite la corrispondenza tra angoli di rotazione al centro nel piano di Mohr e angoli di rotazione del sistema di riferimento Bxy?

6) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del circolo di Mohr che passa per X e Y?

7) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più piccolo tra i circoli di Mohr che passano per l'origine degli assi?

8) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più grande tra i circoli di Mohr che passano per l'origine degli assi?

9) Indicare i punti tensione rappresentativi della componente normale e della componente tangenziale totale di tensione sulle giaciture di versori normali e , facendo uso del polo di Mohr, e rappresentare il corrispondente stato tensionale nel sistema di riferimento di centro B.

10) Quale tra le seguenti affermazioni è vera?

11) Quante sono le direzioni principali di tensione per uno stato tensionale idrostatico?

12) Come si deforma l'intorno materiale di centro B soggetto ad uno stato tensionale idrostatico?

13) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché lo stato tensionale nell'intorno di B sia ancora piano, ma con piano delle tensioni h/z?

14) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché sulla giacitura di normale x si abbia tensione normale nulla?

15) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché sulla giacitura per la quale si ha il massimo della tensione tangenziale totale sia nulla la tensione normale?