I circoli di Mohr per lo stato piano di tensione

I circoli di Mohr per lo stato piano di tensione (test 3)

Prima di affrontare questo test, assicurati di aver chiare le nozioni di: centro di una stella di piani, circoli di Mohr per lo stato triassiale di tensione, componenti speciali di tensione, fascio di piani, giacitura, omotetia, proprietà del polo di Mohr per lo stato di tensione, sostegno di un fascio di piani, stella di piani, stato piano di tensione, stato triassiale di tensione, tensione normale, tensione tangenziale totale, traccia di un piano.

1) Quali punti X e Y del piano di Mohr sono i punti tensione rappresentativi delle componenti normale e tangenziale totale di tensione sulle giaciture di normale x e y?	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
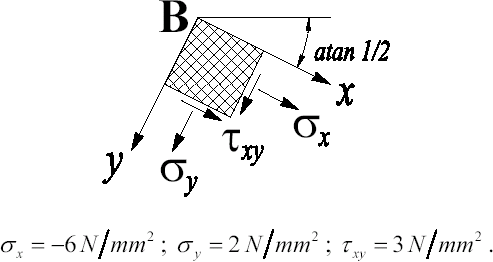
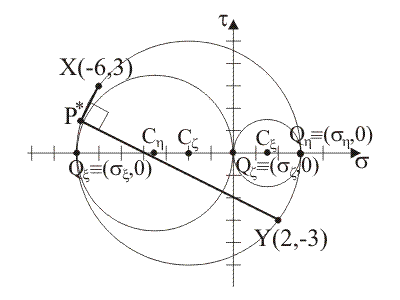
2) Supponendo che i punti tensione del piano di Mohr rappresentativi delle componenti normale e tangenziale totale di tensione sulle giaciture di normale x e y siano, rispettivamente, i punti X≡(–6, 3) e Y≡(2, –3), quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione del polo di Mohr, P, per le giaciture che fanno fascio attorno all'asse z? Coordinate dei centri dei circoli: C_x ≡ (s_{C_x}, t_{C_x}) = (3/2, 0), C_h≡ (s_{C_h}, t_{C_h}) = (–7/2, 0), C_z≡ (s_{C_z}, t_{C_z}) = (–2, 0). Raggi dei circoli: R_x = 3/2, R_h = 7/2, R_z = 5. La retta PX è la retta di equazione t = 2s + 15. La retta PY è la retta di equazione t = –1/2s – 2. Il polo P è il punto di coordinate (s_P, t_P) = (–34/5, 7/5), determinate mettendo in sistema le rette PX e PY. 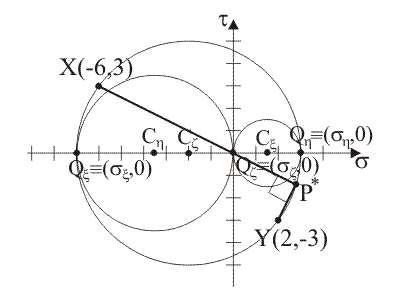Coordinate dei centri dei circoli: C_x ≡ (s_{C_x}, t_{C_x}) = (3/2, 0), C_h≡ (s_{C_h}, t_{C_h}) = (–7/2, 0), C_z≡ (s_{C_z}, t_{C_z}) = (–2, 0). Raggi dei circoli: R_x = 3/2, R_h = 7/2, R_z = 5. La retta PX è la retta di equazione t = –1/2s. La retta PY è la retta di equazione t = 2s – 7. Il polo P* è il punto di coordinate (s_P, t_P) = (14/5, –7/5), determinate mettendo in sistema le rette PX e PY. 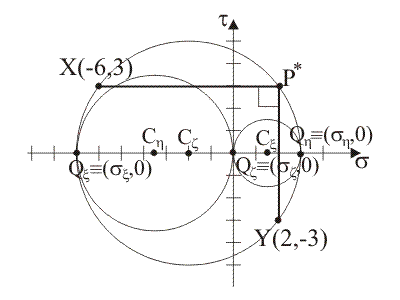Coordinate dei centri dei circoli: C_x ≡ (s_{C_x}, t_{C_x}) = (3/2, 0), C_h≡ (s_{C_h}, t_{C_h}) = (–7/2, 0), C_z≡ (s_{C_z}, t_{C_z}) = (–2, 0). Raggi dei circoli: R_x = 3/2, R_h = 7/2, R_z = 5. La retta PX è la retta di equazione t = 3. La retta PY è la retta di equazione s = 2. Il polo P* è il punto di coordinate (s_P, t_P) = (2, 3), determinate mettendo in sistema le rette PX e PY. 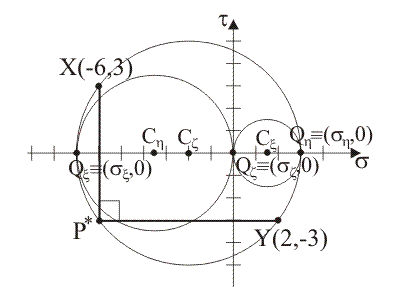Coordinate dei centri dei circoli: C_x ≡ (s_{C_x}, t_{C_x}) = (3/2, 0), C_h≡ (s_{C_h}, t_{C_h}) = (–7/2, 0), C_z≡ (s_{C_z}, t_{C_z}) = (–2, 0). Raggi dei circoli: R_x = 3/2, R_h = 7/2, R_z = 5. La retta PX è la retta di equazione s = –6. La retta PY è la retta di equazione t = –3. Il polo P* è il punto di coordinate (s_P, t_P) = (–6, –3), determinate mettendo in sistema le rette PX e PY.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
3) Quale tra le seguenti affermazioni è corretta per il metodo delle parallele alle tracce delle giaciture? Il polo di Mohr associato alle giaciture del fascio di piani di sostegno z si trova mandando dal punto X≡(s_x, t_xy) la parallela all'asse delle t e dal punto Y≡(s_y, t_yx) la parallela all'asse delle s. Il polo di Mohr associato alle giaciture del fascio di piani di sostegno z si trova mandando dal punto X≡(s_x, t_xy) la parallela all'asse delle y e dal punto Y≡(s_y, t_yx) la parallela all'asse delle x. Il polo di Mohr associato alle giaciture del fascio di piani di sostegno z si trova mandando dal punto X≡(s_x, t_xy) la parallela all'asse delle x e dal punto Y≡(s_y, t_yx) la parallela all'asse delle y. Il polo di Mohr associato alle giaciture del fascio di piani di sostegno z si trova mandando dal punto X≡(s_x, t_xy) la parallela alla traccia (sul piano x/y) della giacitura di normale x e dal punto Y≡(s_y, t_yx) la parallela alla traccia (sul piano x/y) della giacitura di normale y.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
4) Indicare quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione delle direzioni principali di tensione nel piano x/y tramite il polo di Mohr e quali sono la configurazione indeformata e la configurazione deformata dell'elemento di materia le cui facce sono ortogonali alle direzioni trovate. x: direzione principale di compressione h: direzione principale di trazione x: direzione principale di compressione h: direzione principale di trazione x: direzione principale di trazione h: direzione principale di compressione x: direzione principale di trazione h: direzione principale di compressione	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
5) Quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione delle direzioni principali di tensione nel piano x/y tramite la corrispondenza tra angoli di rotazione al centro nel piano di Mohr e angoli di rotazione del sistema di riferimento Bxy?	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
6) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del circolo di Mohr che passa per X e Y? L'asse x. L'asse y. L'asse z. L'asse h.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
7) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più piccolo tra i circoli di Mohr che passano per l'origine degli assi? L'asse x. L'asse y. L'asse h. L'asse x.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
8) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più grande tra i circoli di Mohr che passano per l'origine degli assi? L'asse x. L'asse y. L'asse x. L'asse h.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
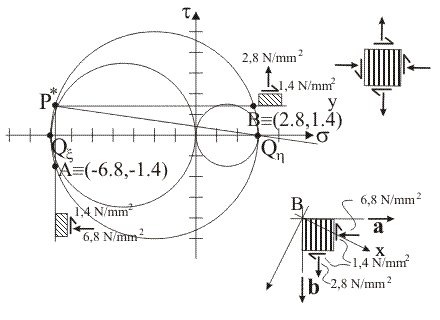
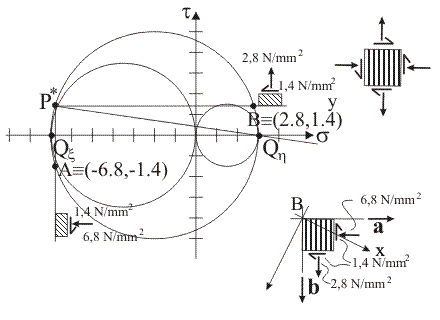
9) Indicare i punti tensione rappresentativi della componente normale e della componente tangenziale totale di tensione sulle giaciture di versori normali e , facendo uso del polo di Mohr, e rappresentare il corrispondente stato tensionale nel sistema di riferimento di centro B. Il punto tensione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale a è il punto A, di coordinate (s_a, t_a) = (–34/5, –7/5): la prima coordinata di A coincide con la prima coordinata di P* e la seconda coordinata di A coincide con l'opposto della seconda coordinata di P. Il punto tensione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale b è il punto B, di coordinate (s_b, t_b) = (14/5, 7/5): la prima coordinata di B si trova dalla relazione s_b= s_{C_z}+ (s_{C_z} – s_P) (ovvero, B è il punto simmetrico di P* rispetto ad una retta verticale che passa per il centro del circolo di cui P* è polo di Mohr) e la seconda coordinata di B coincide con la seconda coordinata di P. 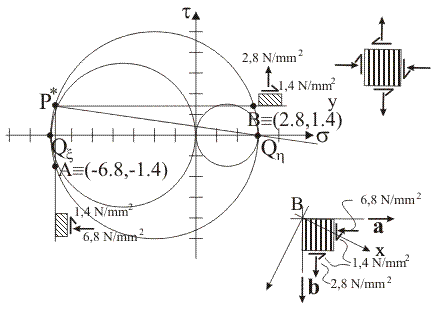Il punto tensione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale a è il punto A, di coordinate (s_a, t_a) = (–34/5, –7/5): la prima coordinata di A coincide con la prima coordinata di P e la seconda coordinata di A coincide con l'opposto della seconda coordinata di P. Il punto tensione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale b è il punto B, di coordinate (s_b, t_b) = (14/5, 7/5): la prima coordinata di B si trova dalla relazione s_b= s_{C_z}+ (s_{C_z} – s_P) (ovvero, B è il punto simmetrico di P* rispetto ad una retta verticale che passa per il centro del circolo di cui P* è polo di Mohr) e la seconda coordinata di B coincide con la seconda coordinata di P. 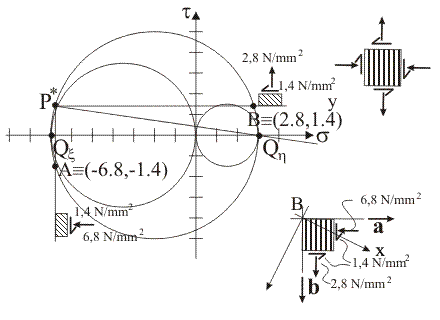Il punto tensione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale a è il punto A, di coordinate (s_a, t_a) = (–34/5, –7/5): la prima coordinata di A coincide con la prima coordinata di P e la seconda coordinata di A coincide con l'opposto della seconda coordinata di P. Il punto 5nsione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale b è il punto B, di coordinate (s_b, t_b) = (14/5, 7/5): la prima coordinata di B si trova dalla relazione s_b= s_{C_z}+ (s_{C_z} – s_P) (ovvero, B è il punto simmetrico di P* rispetto ad una retta verticale che passa per il centro del circolo di cui P* è polo di Mohr) e la seconda coordinata di B coincide con la seconda coordinata di P. Il punto tensione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale a è il punto A, di coordinate (s_a, t_a) = (–34/5, –7/5): la prima coordinata di A coincide con la prima coordinata di P e la seconda coordinata di A coincide con l'opposto della seconda coordinata di P. Il punto tensione rappresentativo delle componenti normale e tangenziale totale di tensione sulla giacitura di versore normale b è il punto B, di coordinate (s_b, t_b) = (14/5, 7/5): la prima coordinata di B si trova dalla relazione s_b= s_{C_z}+ (s_{C_z} – s_P) (ovvero, B è il punto simmetrico di P* rispetto ad una retta verticale che passa per il centro del circolo di cui P* è polo di Mohr) e la seconda 66rdinata di B coincide con la seconda coordinata di P*.	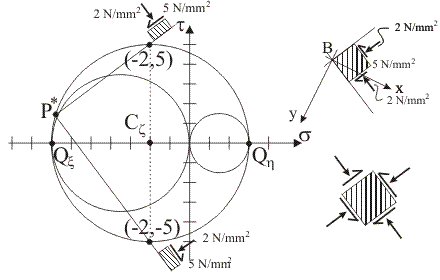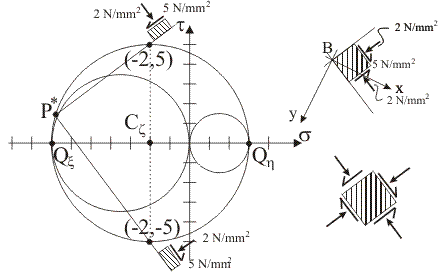Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
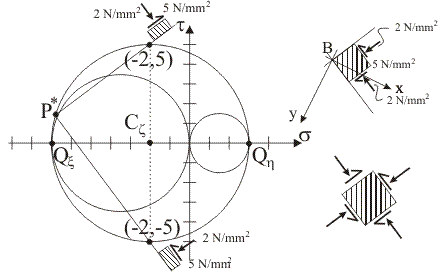
10) Individuare nel piano di Mohr e disegnare nel sistema di riferimento di centro B le tracce delle giaciture della stella di piani di centro B sulle quali è massima la componente tangenziale totale di tensione, facendo uso del polo di Mohr, e valutare il modulo delle componenti speciali di tensione per ognuna delle suddette giaciture. Coordinate dei punti di intersezione tra il circolo di Mohr di sostegno z e le due rette del fascio di centro P* che sono parallele alle tracce delle giaciture cercate: (s_{C_z}, R_z), (s_{C_z}, –R_z). 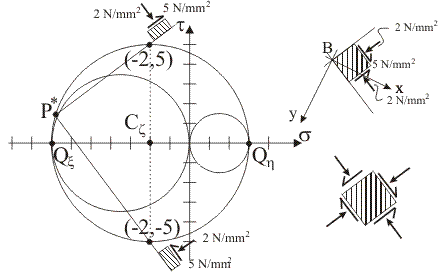Coordinate dei punti di intersezione tra il circolo di Mohr di sostegno z e le due rette del fascio di centro P* che sono parallele alle tracce delle giaciture cercate: (s_{C_z}, R_z), (s_{C_z}, –R_z). Coordinate dei punti di intersezione tra il circolo di Mohr di sostegno z e le due rette del fascio di centro P* che sono parallele alle tracce delle giaciture cercate: (s_{C_z}, R_z), (s_{C_z}, –R_z). Coordinate dei punti di intersezione tra il circolo di Mohr di sostegno z e le due rette del fascio di centro P* che sono parallele alle tracce delle giaciture cercate: (s_{C_z}, R_z), (s_{C_z}, –R_z).	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
11) Che rapporto sussiste tra le direzioni principali di tensione, le tracce delle giaciture sulle quali la tensione normale è nulla e le tracce delle giaciture sulle quali la tensione tangenziale totale è massima? Tra le direzioni principali di tensione, le tracce delle giaciture sulle quali la tensione normale è nulla e le tracce delle giaciture sulle quali la tensione tangenziale totale è massima non è possibile stabilire alcun rapporto. In particolare, le giaciture sulle quali è massima la tensione tangenziale totale non possono mai coincidere con le giaciture sulle quali è nulla la tensione normale e le direzioni principali di tensione non possono mai essere parallele alle giaciture sulle quali è nulla la tensione normale. Le tracce delle giaciture sulle quali la tensione tangenziale totale è massima coincidono con le tracce delle giaciture sulle quali è nulla la componente normale di tensione. Entrambe sono bisettrici degli angoli formati dalle direzioni principali di tensione. Le direzioni principali di tensione sono bisettrici sia degli angoli formati dalle tracce delle giaciture sulle quali la tensione normale è nulla, sia degli angoli formati dalle tracce delle giaciture sulle quali la tensione tangenziale totale è massima. In particolare, nell'elemento piano di materia le cui facce sono parallele alle tracce delle giaciture sulle quali la tensione normale è nulla, le diagonali individuano le direzioni principali di tensione e le bisettrici degli angoli formati dalle diagonali individuano le tracce delle giaciture sulle quali la tensione tangenziale totale è massima. Gli angoli formati dalle direzioni principali di tensione con le tracce delle giaciture sulle quali la tensione tangenziale totale è massima sono sempre di 45°, mentre gli angoli formati dalle direzioni principali di tensione con le tracce delle giaciture sulle quali la tensione normale è nulla sono di 45° solo se il centro del circolo coincide con l'origine. In questo caso, le giaciture sulle quali la tensione normale è nulla coincidono con le giaciture sulle quali si ha tensione tangenziale totale massima. Invece, quando il circolo è tangente all'origine, le giaciture sulle quali la tensione normale è nulla diventano parallele alle direzioni principali di tensione. In altre parole, aggiungendo uno stato tensionale idrostatico, si modificano solo le giaciture sulle quali la tensione normale è nulla, mentre non si alterano le direzioni principali di tensione e le giaciture a tensione tangenziale totale massima. Le tracce delle giaciture sulle quali la tensione tangenziale totale è massima sono ortogonali alle tracce delle giaciture sulle quali è nulla la componente normale di tensione. Entrambe sono bisettrici degli angoli formati dalle direzioni principali di tensione.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
12) Come si deforma l'elemento di materia di centro B soggetto ad uno stato tensionale tangenziale puro? L'elemento si deforma variando di volume e mantenendo la forma originaria. Le sue facce traslano senza ruotare. Gli spigoli si muovono lungo rette parallele alle facce. L'elemento si deforma variando sia di volume che di forma. Le sue facce traslano e ruotano attorno al proprio baricentro. Gli spigoli si muovono lungo le direzioni principali di tensione. L'elemento si deforma variando di forma e mantenendo il volume originario. Le sue facce ruotano attorno al proprio baricentro, senza traslare. Gli spigoli si muovono lungo le direzioni principali di tensione. L'elemento non varia né di volume né di forma. Le sua facce non traslano e non ruotano. Gli spigoli non si muovono.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
13) Rappresentare nel piano di Mohr il tensore idrostatico e il tensore deviatorico per lo stato tensionale assegnato sulle giaciture della stella di piani di centro B.	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
14) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché le due giaciture del fascio di sostegno z sulle quali è nulla la componente normale di tensione siano ortogonali? s_I = –R_x s_I = R_z–2R_x s_I = R_h s_I = 2R_h	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
15) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché le due giaciture del fascio di sostegno z sulle quali è nulla la componente normale di tensione coincidano? s_I = –2R_h s_I = 2R_h s_I = –2R_x s_I = 2R_x	Il browser in uso non supporta frame non ancorati oppure è configurato in modo che i frame non ancorati non siano visualizzati.
	Punteggio ottenuto: / 30

I circoli di Mohr per lo stato piano di tensione (test 3)

1) Quali punti X e Y del piano di Mohr sono i punti tensione rappresentativi delle componenti normale e tangenziale totale di tensione sulle giaciture di normale x e y?

3) Quale tra le seguenti affermazioni è corretta per il metodo delle parallele alle tracce delle giaciture?

5) Quale tra le seguenti rappresentazioni illustra la corretta costruzione grafica per la determinazione delle direzioni principali di tensione nel piano x/y tramite la corrispondenza tra angoli di rotazione al centro nel piano di Mohr e angoli di rotazione del sistema di riferimento Bxy?

6) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del circolo di Mohr che passa per X e Y?

7) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più piccolo tra i circoli di Mohr che passano per l'origine degli assi?

8) Qual è il sostegno delle giaciture le cui componenti speciali di tensione sono rappresentate dalle coordinate dei punti del più grande tra i circoli di Mohr che passano per l'origine degli assi?

9) Indicare i punti tensione rappresentativi della componente normale e della componente tangenziale totale di tensione sulle giaciture di versori normali e , facendo uso del polo di Mohr, e rappresentare il corrispondente stato tensionale nel sistema di riferimento di centro B.

11) Che rapporto sussiste tra le direzioni principali di tensione, le tracce delle giaciture sulle quali la tensione normale è nulla e le tracce delle giaciture sulle quali la tensione tangenziale totale è massima?

12) Come si deforma l'elemento di materia di centro B soggetto ad uno stato tensionale tangenziale puro?

13) Rappresentare nel piano di Mohr il tensore idrostatico e il tensore deviatorico per lo stato tensionale assegnato sulle giaciture della stella di piani di centro B.

14) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché le due giaciture del fascio di sostegno z sulle quali è nulla la componente normale di tensione siano ortogonali?

15) Qual è la quota di stato tensionale idrostatico da aggiungere allo stato piano assegnato affinché le due giaciture del fascio di sostegno z sulle quali è nulla la componente normale di tensione coincidano?