 |
Azioni esterne di tipo coppia concentrate sui nodi
Prima di affrontare questo
argomento, assicurati di aver chiare le nozioni di:
coppia,
diagrammi delle caratteristiche di sollecitazione interna, equilibrio, equivalenza,
metodo delle forze,
metodo dei telai a nodi spostabili,
nodo, principio di azione e reazione.
|
Generalità
Sia consideri
un'azione esterna
 di tipo coppia, applicata in
corrispondenza della sezione H
del tronco i-j
in Fig. 1. Per tracciare il diagramma del momento flettente in
corrispondenza della sezione sede dell'azione esterna
di tipo coppia, applicata in
corrispondenza della sezione H
del tronco i-j
in Fig. 1. Per tracciare il diagramma del momento flettente in
corrispondenza della sezione sede dell'azione esterna
 ,
si operino due tagli nell'intorno di H, uno a sinistra e uno a destra di
H,
entrambi a distanza infinitesima da H. Nell'ipotesi che il tronco i-j
appartenga ad una struttura in equilibrio, il tronco ed ogni sua porzione devono
risultare in equilibrio. Dunque, anche il concio infinitesimo racchiuso tra la
sezione a sinistra e la sezione a destra di H deve risultare in equilibrio.
,
si operino due tagli nell'intorno di H, uno a sinistra e uno a destra di
H,
entrambi a distanza infinitesima da H. Nell'ipotesi che il tronco i-j
appartenga ad una struttura in equilibrio, il tronco ed ogni sua porzione devono
risultare in equilibrio. Dunque, anche il concio infinitesimo racchiuso tra la
sezione a sinistra e la sezione a destra di H deve risultare in equilibrio.
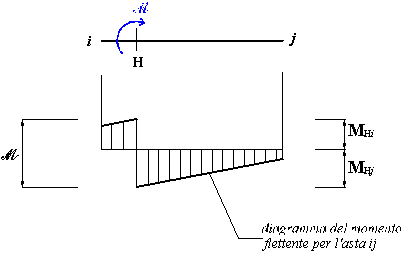
Fig. 1
Estraiamo il
concio infinitesimo ricavato nell'intorno di H, senza alterarne lo stato di
sollecitazione. Affinché ciò si realizzi, occorre applicare sulle facce del
concio estratto le azioni che venivano trasmesse al concio, prima del
sezionamento, dai tronchi i-H e H-j. Queste azioni, che, prima del
sezionamento, erano azioni interne, diventano azioni esterne nel momento in cui
vengono messe in evidenza sulla facce del concio estratto. In altre parole,
occorre introdurre dall'esterno, come azioni esterne, quelle forze che i tronchi
i-H e H-j non sono più in grado di trasferire al concio, come
azioni interne, essendo stati separati dal concio.
Dovendo ricavare
delle informazioni utili al tracciamento del diagramma del momento flettente,
tra tutte le azioni trasmesse al concio prima del sezionamento verranno
considerate, nel seguito, solo quelle che influiscono sul diagramma del momento
flettente, trascurando lo sforzo normale N (Fig. 2). Le azioni in questione sono:
le due azioni
 e
e
 trasmesse dal tronco i-H sulla faccia di sinistra del concio, le due
azioni
trasmesse dal tronco i-H sulla faccia di sinistra del concio, le due
azioni
 e
e
 trasmesse dal tronco H-j sulla faccia di destra del concio e l'azione
esterna
trasmesse dal tronco H-j sulla faccia di destra del concio e l'azione
esterna
 .
.
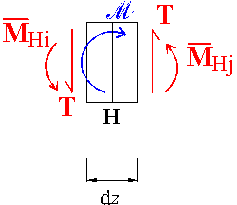
Fig. 2
Dall'equilibrio alla traslazione
verticale del concio, segue che le due azioni
 e
e
 devono essere uguali in modulo e opposte in verso (Fig. 2):
devono essere uguali in modulo e opposte in verso (Fig. 2):
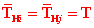 .
.
Inoltre,
assumendo positivi i momenti antiorari,
l’equilibrio alla rotazione del concio rispetto ad un qualunque punto della
sezione H impone che sia soddisfatta la relazione (Fig. 2):
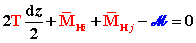
dove
 e
e
 ,
momenti agenti sulle facce del concio infinitesimo, sono entrambi discordi
rispetto alla coppia
,
momenti agenti sulle facce del concio infinitesimo, sono entrambi discordi
rispetto alla coppia
 . Per le
dimensioni infinitesime del concio, il primo termine dell'equazione che
esprime l'equilibrio alla rotazione è un infinitesimo.
Trascurando il termine infinitesimo nei confronti degli altri tre
contributi, si
può esprimere l'equilibrio alla rotazione del concio nella forma:
. Per le
dimensioni infinitesime del concio, il primo termine dell'equazione che
esprime l'equilibrio alla rotazione è un infinitesimo.
Trascurando il termine infinitesimo nei confronti degli altri tre
contributi, si
può esprimere l'equilibrio alla rotazione del concio nella forma:
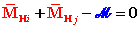 .
(equilibrio sul concio)
.
(equilibrio sul concio)
Per
il principio di azione e reazione, i momenti MHi
e MHj
che il concio trasmette ai tronchi i-H e H-j sono uguali in modulo
e opposti in verso rispetto ai momenti
 e
e
 che i
tronchi i-H e H-j trasmettono al concio. Dunque, i momenti
MHi
e MHj
sono entrambi concordi rispetto alla coppia
che i
tronchi i-H e H-j trasmettono al concio. Dunque, i momenti
MHi
e MHj
sono entrambi concordi rispetto alla coppia
 e soddisfano la
relazione di equivalenza:
e soddisfano la
relazione di equivalenza:
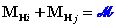 .
(equivalenza sui tronchi afferenti al concio)
.
(equivalenza sui tronchi afferenti al concio)
Poiché le azioni
che vanno considerate ai fini del tracciamento del diagramma del momento
flettente in H sono
quelle sui tronchi afferenti al concio
sede dell'azione esterna
 (MHi
e MHj),
possiamo concludere che il momento flettente sulla
sezione H del tronco H-i (MHi,
modulo di MHi)
differisce dal momento flettente sulla sezione H del tronco H-j (MHj,
modulo di MHj)
per la quantità
(MHi
e MHj),
possiamo concludere che il momento flettente sulla
sezione H del tronco H-i (MHi,
modulo di MHi)
differisce dal momento flettente sulla sezione H del tronco H-j (MHj,
modulo di MHj)
per la quantità
 , momento
della coppia concentrata su H.
Come mostrato in Fig. 1, allora, il diagramma del momento flettente subisce in H una
discontinuità nel valore (discontinuità di prima specie), ma non nella tangente
(discontinuità di seconda specie). Infatti, ricordando che il taglio, derivata
prima del momento flettente:
, momento
della coppia concentrata su H.
Come mostrato in Fig. 1, allora, il diagramma del momento flettente subisce in H una
discontinuità nel valore (discontinuità di prima specie), ma non nella tangente
(discontinuità di seconda specie). Infatti, ricordando che il taglio, derivata
prima del momento flettente:
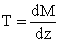 ,
,
è costante in H per
l'equilibrio alla traslazione verticale del concio, anche la
pendenza del diagramma del momento flettente deve essere costante in H.
Stabilendo di indicare col termine "azioni interne" le azioni
sui tronchi,
possiamo esprimere a parole la relazione di equivalenza sui tronchi afferenti al
concio dicendo che, sul generico tronco sede
di una o più azioni esterne di tipo coppia, la somma vettoriale delle azioni
interne di tipo coppia (nel nostro caso, MHi
e MHj)
deve essere uguale, in modulo e verso, alla somma
vettoriale
delle azioni esterne
di tipo coppia
(nel nostro caso,
 ).
).
Se la somma
vettoriale delle azioni esterne di tipo coppia è una
coppia nulla:
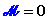
dalla
relazione di equivalenza si deduce
che i due momenti MHi
e MHj
devono avere stesso modulo e verso discorde.
Il
risultato ottenuto è indipendente dalla posizione della sezione H. Pertanto,
esso vale anche per coppie
 applicate in corrispondenza dei nodi di estremità.
applicate in corrispondenza dei nodi di estremità.
Metodo delle forze e metodo dei telai a nodi spostabili: svincolamento alla rotazione in una sezione sede di
un'azione esterna di tipo coppia
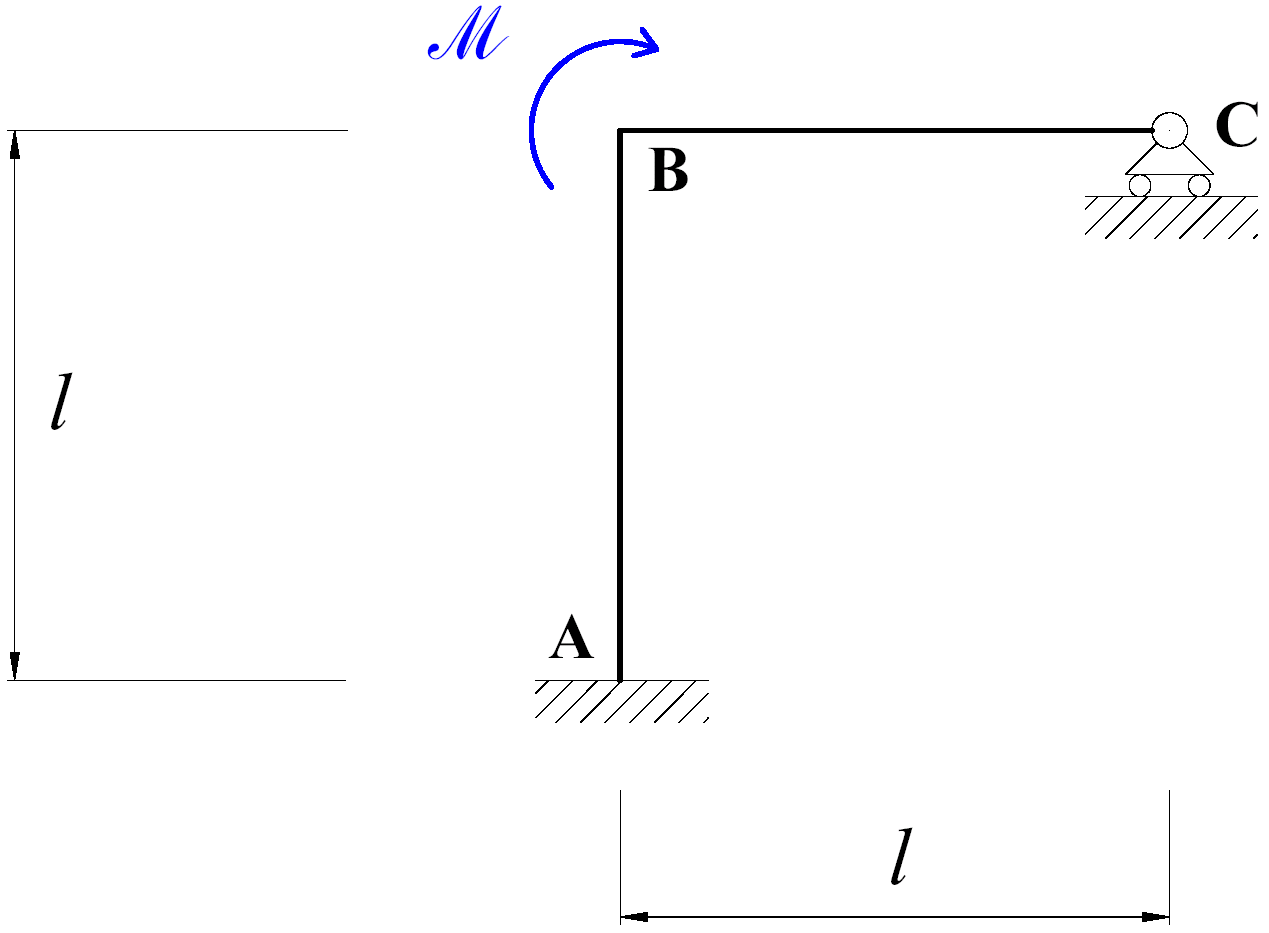
Fig. 3
Nel nodo B della struttura in Fig. 3, è applicata una coppia esterna
 . Dunque, per quanto
visto nelle Generalità, il diagramma del momento
flettente subisce in
B una discontinuità in valore.
. Dunque, per quanto
visto nelle Generalità, il diagramma del momento
flettente subisce in
B una discontinuità in valore.
Svincolando alla rotazione il nodo
B,
come richiesto dal metodo dei telai a nodi spostabili (Fig.
4), e mettendo in evidenza i momenti agenti nelle aste BA e BC
(incognite iperstatiche), sarà quindi necessario introdurre in B due differenti incognite iperstatiche,
Y e Z.
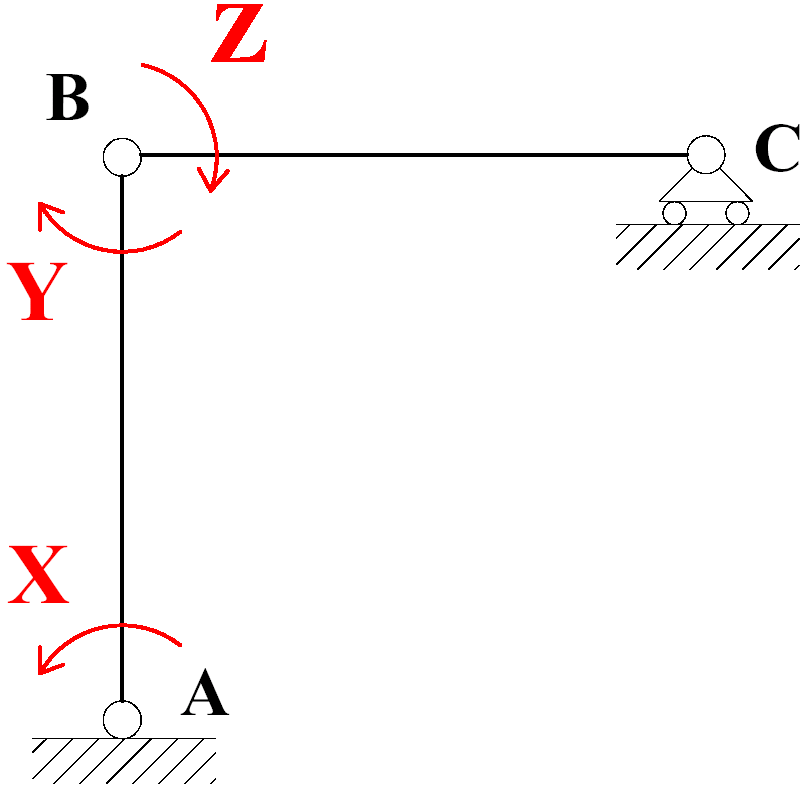
Fig. 4
Analogamente a quanto visto
nelle Generalità (Figg. 1 e 2), il legame tra i momenti
incogniti Y e Z
si ricava dall’equilibrio alla rotazione del nodo B, sede della coppia esterna
 , che può essere
isolato dalla struttura operando un taglio subito a destra di B e un taglio
subito al di sotto di B (Fig. 5).
, che può essere
isolato dalla struttura operando un taglio subito a destra di B e un taglio
subito al di sotto di B (Fig. 5).
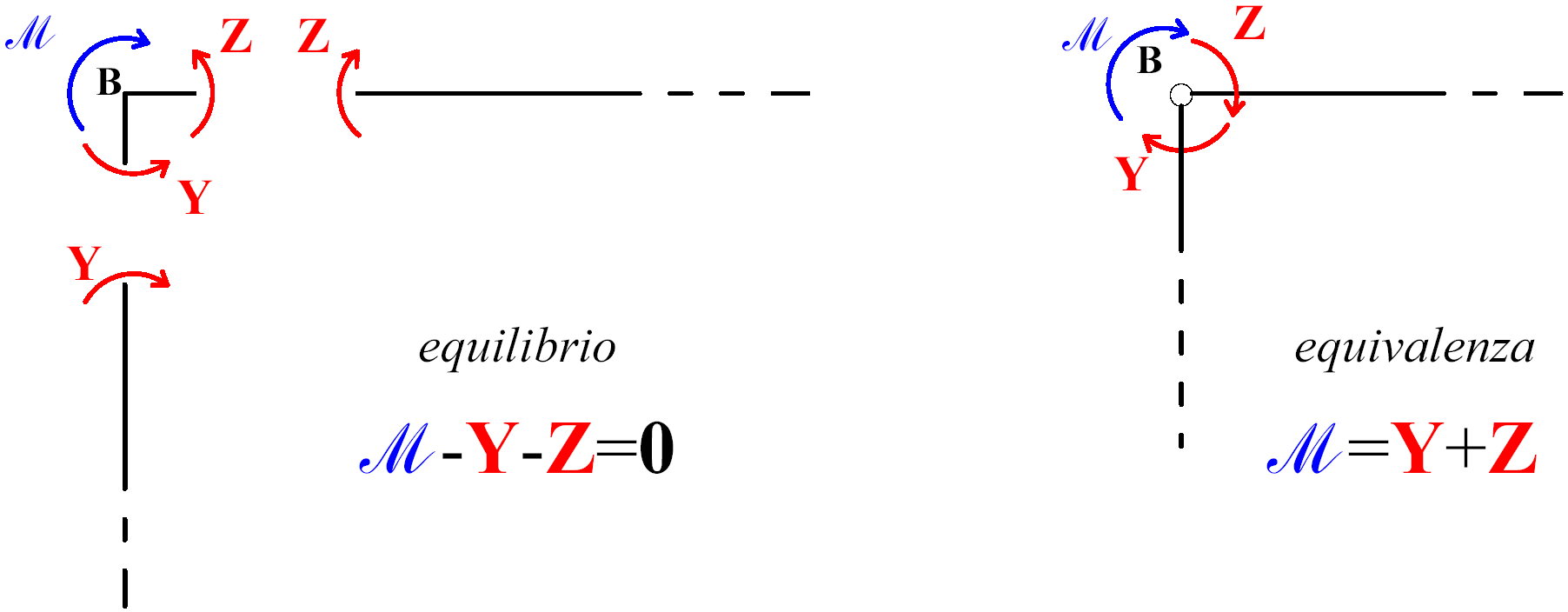
Fig. 5
Per l'equilibrio del nodo
B
(Fig.
5), le azioni agenti sul nodo devono equilibrarsi, ovvero, devono costituire un
sistema nullo.
Assumendo positivi i momenti orari, l'equilibrio alla rotazione del nodo B
impone:

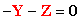 (equilibrio)
(equilibrio)
dove
Y
e
Z
sono i momenti agenti sul nodo B. Tale relazione di equilibrio può essere messa
nella forma:

con
la quale si stabilisce il legame di dipendenza tra i momenti
Y
e
Z.
Ai momenti
Y
e Z agenti sul nodo, la cui somma vettoriale
equilibra
la coppia
 ,
il principio di azione e reazione fa corrispondere
i momenti
Y
e Z agenti sulle aste, la cui somma vettoriale equivale
all’azione esterna
,
il principio di azione e reazione fa corrispondere
i momenti
Y
e Z agenti sulle aste, la cui somma vettoriale equivale
all’azione esterna
 .
Dunque, il problema della ricerca della relazione di dipendenza tra i momenti
Y
e Z,
risolto in termini di equilibrio ragionando sul nodo sede della coppia
esterna, può essere risolto anche in termini di equivalenza, ragionando sulle aste che afferiscono al nodo. Ovvero, intendendo per azioni
interne quelle agenti sulle aste, il legame tra
Y
e Z
può essere determinato osservando che, in ogni nodo, la somma delle azioni esterne deve
sempre essere equivalente alla somma delle azioni interne (v. Generalità). Dalla Fig.
5, si ricava (per equivalenza):
.
Dunque, il problema della ricerca della relazione di dipendenza tra i momenti
Y
e Z,
risolto in termini di equilibrio ragionando sul nodo sede della coppia
esterna, può essere risolto anche in termini di equivalenza, ragionando sulle aste che afferiscono al nodo. Ovvero, intendendo per azioni
interne quelle agenti sulle aste, il legame tra
Y
e Z
può essere determinato osservando che, in ogni nodo, la somma delle azioni esterne deve
sempre essere equivalente alla somma delle azioni interne (v. Generalità). Dalla Fig.
5, si ricava (per equivalenza):


dove
Y
e
Z
sono i momenti agenti sulle aste BA e BC.
In virtù della condizione di equivalenza, la coppia esterna
 si distribuisce tra le aste BC e BA. Ovvero, una
parte della coppia si ripartisce sull'asta BA (Y)
e la restante parte si ripartisce sull'asta BC (M-Y). Poiché l’asta BA
“vede” la coppia esterna solo per la quota Y,
trasmessa dal nodo B, e l’asta BC “vede” la coppia esterna solo per la
quota M -Y,
trasmessa ancora dal nodo B, il problema in Fig. 3 può essere ricondotto allo
studio della struttura di Fig. 6, in cui la coppia
si distribuisce tra le aste BC e BA. Ovvero, una
parte della coppia si ripartisce sull'asta BA (Y)
e la restante parte si ripartisce sull'asta BC (M-Y). Poiché l’asta BA
“vede” la coppia esterna solo per la quota Y,
trasmessa dal nodo B, e l’asta BC “vede” la coppia esterna solo per la
quota M -Y,
trasmessa ancora dal nodo B, il problema in Fig. 3 può essere ricondotto allo
studio della struttura di Fig. 6, in cui la coppia
 compare direttamente
secondo le proprie quote di ripartizione sulle aste BA e BC.
compare direttamente
secondo le proprie quote di ripartizione sulle aste BA e BC.
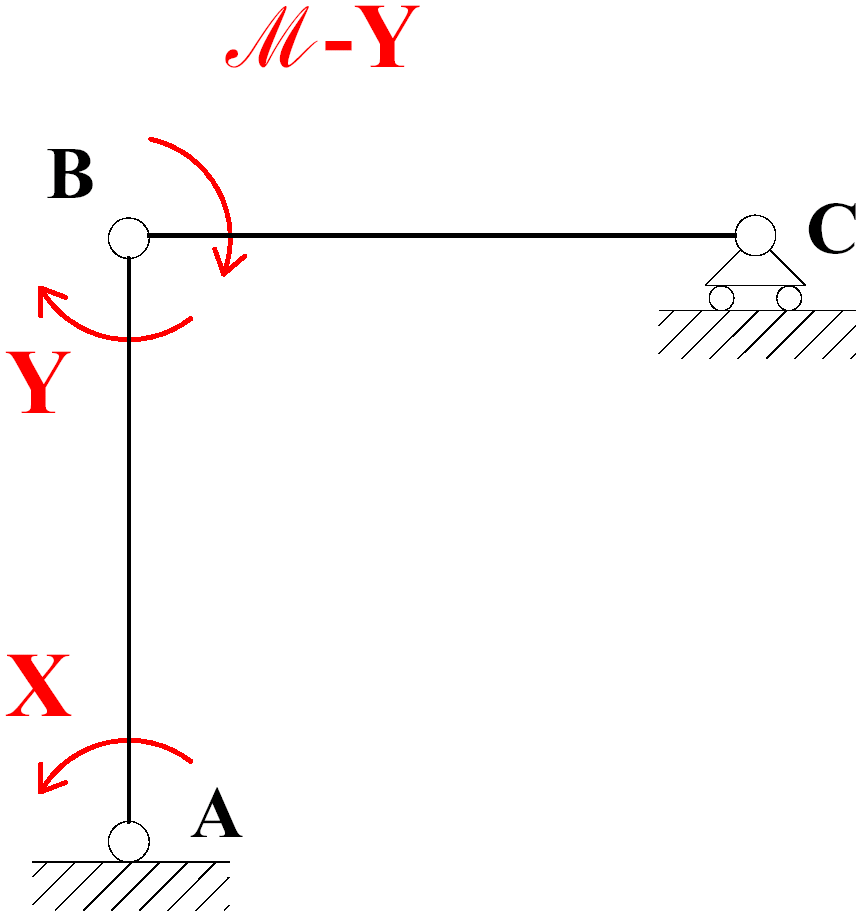
Fig. 6
Si osservi come soddisfare a priori l’equilibrio del nodo B porti a
stabilire un legame di dipendenza tra 2 incognite iperstatiche (Y
e Z). Ciò fa sì che il numero delle
incognite indipendenti in Fig. 4 non sia 3 (X,
Y, Z),
ma 2 e porta alla scrittura di un’equazione in meno nel sistema
risolvente. In generale, soddisfare a priori
l’equilibrio in n nodi riduce di n il numero delle incognite iperstatiche.
Test di verifica dell'apprendimento:
