 |
I telai a nodi spostabili
Prima di affrontare questo argomento, assicurati di aver chiare le nozioni di:
applicazione del P.L.V. ai corpi rigidi,
azioni esterne di tipo coppia concentrate sui nodi,
caratteristiche di sollecitazione interna,
composizione cinematica delle rotazioni e degli
spostamenti, componenti assolute di spostamento generalizzato, componenti
relative di spostamento generalizzato,
coppia,
equazioni di congruenza, equazioni di
equilibrio, grado di vincolo, incognite iperstatiche, ipotesi di piccoli
spostamenti, lavoro, metodo delle forze, molteplicità di vincolo,
momento di una coppia, principio di sovrapposizione degli effetti, telaio, vincolo
cedevole, vincolo rigido.
|
Generalità
Si definisce telaio a nodi spostabili un telaio in cui i nodi, oltre a
ruotare, possono anche traslare. Se non si trascura la deformabilità assiale,
ogni
telaio risulta sempre a nodi spostabili.
Per valutare se un telaio è a nodi fissi o a nodi spostabili, si considera il
grado di vincolo della struttura che si ottiene inserendo una cerniera in
corrispondenza di ogni nodo interno ed esterno in cui risulti vincolata la
rotazione (assoluta o relativa), sia che essa sia vincolata in modo perfetto
(vincolo rigido), sia che essa sia vincolata solo parzialmente (vincolo
cedevole). Come per il metodo delle forze, la struttura svincolata e caricata
nelle sezioni di svincolamento con le azioni trasmesse dai gradi di vincolo
soppressi (incognite iperstatiche), assunte con
verso arbitrario, viene detta
travatura reticolare associata. Se la travatura reticolare associata è isostatica o iperstatica, il telaio è a nodi fissi.
Al contrario, se la travatura reticolare
associata è labile, il telaio è a nodi spostabili. In questo caso,
il grado di labilità della travatura reticolare associata è uguale al numero di
nodi spostabili.
Occorre precisare che il numero di nodi spostabili non corrisponde al numero di
nodi che effettivamente si spostano, ma al numero di parametri indipendenti che
definiscono la deformata rigida della travatura reticolare associata. Ovvero, il
numero di nodi spostabili restituisce il numero di atti di moto rigido della
travatura reticolare associata e corrisponde al numero di vincoli semplici che
occorre introdurre per rendere a nodi fissi il telaio a nodi spostabili. In
generale, il numero di nodi che si spostano è maggiore o uguale al numero
di nodi spostabili.
Ognuna delle deformate per moto rigido che si ottengono da una travatura
reticolare associata labile attivando un parametro indipendente di spostamento
alla volta prende il nome di “cinematismo elementare” o “meccanismo”.
In sostanza, in un telaio a nodi spostabili si hanno tanti cinematismi
elementari quanti sono i gradi di labilità (nodi spostabili) della travatura
reticolare associata.
Nel metodo dei telai a nodi spostabili,
le incognite sono rappresentate dai
momenti e dagli spostamenti indipendenti nei nodi del telaio a nodi spostabili.
Esse si determinano aggiungendo alle equazioni di
congruenza, scritte per ogni nodo
in cui si operi uno svincolamento alla rotazione (assoluta o relativa), tante equazioni di equilibrio quanti sono i parametri indipendenti di
spostamento. Il metodo dei telai a nodi spostabili è il metodo più
automatico ma, in generale, non il più conveniente per risolvere un telaio a
nodi spostabili.
Il metodo dei telai a nodi spostabili
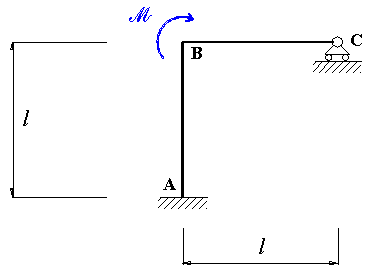
Fig. 1
Il telaio in Fig. 1 è una volta iperstatico.
La sua travatura reticolare
associata, mostrata in Fig. 2, è una volta labile. Dunque, la struttura in Fig. 1 è un telaio a
un
nodo spostabile.
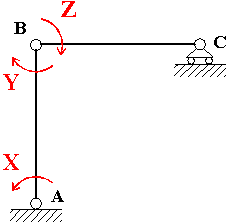
Fig. 2
Poiché nel nodo B è applicata una coppia esterna
 , il diagramma del momento flettente subisce in B una discontinuità pari a
, il diagramma del momento flettente subisce in B una discontinuità pari a
 ,
momento della
coppia
,
momento della
coppia
 (v. scheda sulle azioni esterne di tipo coppia concentrate sui nodi).
Dunque, nel sostituire al grado di vincolo alla rotazione relativa in B le
azioni, assunte con verso arbitrario, che il grado di vincolo soppresso trasmetteva
alle aste AB e BC prima di
essere tolto (i momenti agli estremi B delle aste AB e BC), è necessario introdurre due differenti incognite iperstatiche,
Y e Z,
per tener conto della discontinuità in valore del diagramma del momento
flettente in B. Come
mostrato nella scheda dedicata alle
azioni esterne di tipo coppia concentrate sui nodi,
stabilendo di indicare col termine "azioni interne" le azioni sulle aste, per l'equilibrio alla rotazione del concio sede di un'azione esterna di tipo coppia
le azioni interne sono concordi all'azione esterna e la loro somma (vettoriale) è uguale,
in modulo e verso, all'azione esterna (equivalenza sulle aste afferenti al nodo, Fig. 3):
(v. scheda sulle azioni esterne di tipo coppia concentrate sui nodi).
Dunque, nel sostituire al grado di vincolo alla rotazione relativa in B le
azioni, assunte con verso arbitrario, che il grado di vincolo soppresso trasmetteva
alle aste AB e BC prima di
essere tolto (i momenti agli estremi B delle aste AB e BC), è necessario introdurre due differenti incognite iperstatiche,
Y e Z,
per tener conto della discontinuità in valore del diagramma del momento
flettente in B. Come
mostrato nella scheda dedicata alle
azioni esterne di tipo coppia concentrate sui nodi,
stabilendo di indicare col termine "azioni interne" le azioni sulle aste, per l'equilibrio alla rotazione del concio sede di un'azione esterna di tipo coppia
le azioni interne sono concordi all'azione esterna e la loro somma (vettoriale) è uguale,
in modulo e verso, all'azione esterna (equivalenza sulle aste afferenti al nodo, Fig. 3):


con
Y
e
Z
coppie agenti sulle aste AB e BC.
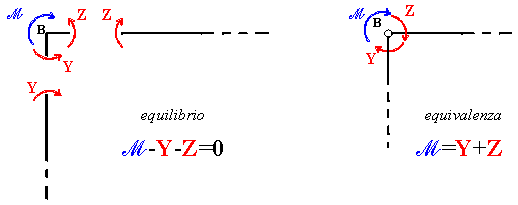
Fig. 3
Per la condizione di equivalenza sulle aste afferenti al nodo B
(Fig. 3), la coppia esterna
 si ripartisce sulle aste AB
e BC, nel senso che una
parte della coppia
si ripartisce sulle aste AB
e BC, nel senso che una
parte della coppia
 viene trasmessa dal nodo B all'asta BA (Y)
e la restante parte viene trasmessa dal nodo B all'asta BC (
viene trasmessa dal nodo B all'asta BA (Y)
e la restante parte viene trasmessa dal nodo B all'asta BC (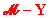 ). Poiché l’asta AB
“vede” la coppia esterna
). Poiché l’asta AB
“vede” la coppia esterna
 solo per la quota Y,
trasmessa all'asta dal nodo B, e l’asta BC “vede” la coppia esterna
solo per la quota Y,
trasmessa all'asta dal nodo B, e l’asta BC “vede” la coppia esterna
 solo per la
quota
solo per la
quota
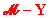 ,
trasmessa ancora dal nodo B, il problema in Fig. 1 può essere ricondotto allo
studio della struttura di Fig. 4, in cui la coppia
,
trasmessa ancora dal nodo B, il problema in Fig. 1 può essere ricondotto allo
studio della struttura di Fig. 4, in cui la coppia
 compare direttamente
secondo le proprie quote di ripartizione sulle aste AB e BC.
compare direttamente
secondo le proprie quote di ripartizione sulle aste AB e BC.
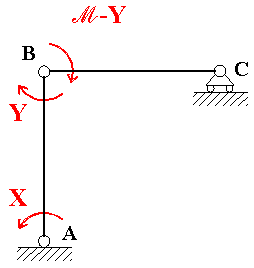
Fig. 4
Si osservi come soddisfare a priori l’equilibrio del nodo B porti a
stabilire un legame di dipendenza tra 2 incognite iperstatiche (Y
e Z). Ciò fa sì che il numero delle
incognite indipendenti in Fig. 2 non sia 3 (X,
Y, Z),
ma 2 e porta alla scrittura di un’equazione in meno nel sistema
risolvente. In generale, soddisfare a priori
l’equilibrio in n nodi riduce di n il numero delle incognite iperstatiche.
Proseguendo nella risoluzione dell’esercizio, si devono imporre le condizioni
di congruenza nelle sezioni di svincolamento alla rotazione, per assicurare che
la travatura reticolare associata, oltre ad essere staticamente equivalente (per
l'ipotesi che le incognite iperstatiche siano uguali alle reazioni dei vincoli
soppressi), sia anche cinematicamente equivalente al telaio in Fig. 1.
In altre parole, tra tutte le infinite coppie di valori
X e Y che lasciano in
equilibrio la travatura reticolare associata, quella
che risolve il problema è l’unica per la quale la struttura si
deforma rispettando i vincoli interni ed esterni:
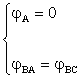
Nell'esplicitare le condizioni di congruenza nei nodi A e B, bisogna tener conto del contributo
alla rotazione in A e B che deriva dal cinematismo associato al telaio a un nodo
spostabile. Il cinematismo elementare che si ottiene assegnando un
valore arbitrario (d) al parametro
libero di
spostamento per atto di moto rigido della travatura reticolare associata è riportato in
nero in Fig. 5.
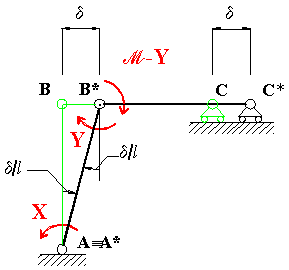
Fig. 5
Per le condizioni di vincolo sulla travatura reticolare
associata (Fig. 5), i nodi B e C possono traslare solo in
direzione orizzontale.
A chiarimento della differenza che sussiste tra numero di nodi spostabili e
numero di nodi che si spostano (introdotta nelle
Generalità), si osservi come nel cinematismo a un solo nodo spostabile di
Fig. 5 i nodi che si spostano siano ben 2: il nodo B e il nodo C.
Come precisato nelle Generalità, infatti, il numero di
nodi spostabili rappresenta il numero di gradi di libertà per atto di moto rigido della
travatura reticolare associata, e non
il numero di nodi che effettivamente si spostano. In effetti, una volta fissato lo spostamento
arbitrario d da assegnare al nodo B
(C), lo spostamento del secondo nodo che si sposta nel meccanismo di Fig.
5, il nodo C (B),
rimane identificato da d
per il fatto che, essendo una deformata per atto di moto rigido, il meccanismo è definito a meno di tutte le componenti di
spostamento che derivano dalla deformabilità elastica del telaio, comprese
quelle legate alla deformabilità assiale del tratto BC. Di conseguenza,
l'asta BC trasla rigidamente senza variare di lunghezza. Nell'ambito della
teoria dei piccoli spostamenti, ciò implica che la componente di spostamento del
nodo C(B) lungo la congiungente B con C sia uguale
alla componente di spostamento del nodo B(C), sempre lungo la
congiungente B con C. In altre parole, l'inestensibilità delle
aste impone un vincolo di rigidità tra le componenti di spostamento dei nodi,
valutate lungo la congiungente i nodi (componenti di spostamento assiale). Il
vincolo di rigidità stabilisce una relazione di dipendenza tra le componenti di
spostamento assiale. Ciò fa si che il numero di parametri liberi (indipendenti)
che definiscono la deformata rigida della travatura reticolare associata sia
inferiore al numero di componenti di spostamento. La differenza tra componenti
di spostamento e parametri liberi di spostamento è uguale al numero di aste che
ammettono una traslazione rigida in direzione assiale.
In conclusione,
pur essendo 2 i nodi che si spostano, il parametro indipendente di
spostamento che definisce la deformata rigida della travatura reticolare
associata in Fig. 5, e, quindi, il nodo spostabile, è solo uno.
Assumendo positive le rotazioni se orarie, le relazioni che
esprimono la congruenza nei nodi A e B
sono le seguenti 2 equazioni
scalari nelle 3 incognite X,
Y e
d
(spostamento del nodo B):
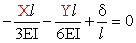
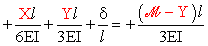 .
.
L’ulteriore equazione da scrivere per uguagliare il numero di equazioni al
numero di incognite si ricava da una condizione di
equilibrio. Il modo più automatico per scrivere
l’equazione di equilibrio mancante è quello di utilizzare il P.L.V., assumendo
come sistema deformante (o degli spostamenti) il cinematismo associato e come sistema
lavorante (o delle forze)
quello reale. La relazione che ne deriva
prende il nome di equazione di catena.
Come chiarito nelle Generalità,
il numero di equazioni di equilibrio, o di catena, da aggiungere alle
equazioni di congruenza è uguale al numero di nodi spostabili. Inoltre,
poiché, per definizione, un cinematismo è la deformata rigida di una
struttura labile, le caratteristiche di
sollecitazione interna sono identicamente nulle nelle travature
reticolari associate di tutti i telai a nodi spostabili. Di conseguenza, il lavoro virtuale interno
di un meccanismo è sempre nullo
(applicazione del P.L.V. ai corpi
rigidi).
Assegnato uno
spostamento virtuale
d
al nodo B in Fig. 5,
il P.L.V. applicato ai corpi rigidi porta a scrivere i seguenti termini di
lavoro:
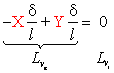
da cui,
semplificando il parametro libero
d
e moltiplicando per l, si ricava una relazione tra X
e
Y, ovvero, un'equazione di equilibrio:
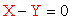 .
.
Nella fattispecie, la relazione ottenuta semplificando l'equazione di
catena esprime l'equilibrio alla rotazione dell’asta AB.
Mettendo in sistema le due equazioni di congruenza e l'equazione di equilibrio,
si ricavano i
valori delle incognite iperstatiche e dello spostamento orizzontale del nodo
B:
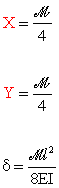
Il diagramma del momento flettente è riportato in Fig. 6.

Fig. 6
Risoluzione dei telai a nodi spostabili con il metodo delle forze
La struttura una volta iperstatica in Fig. 1 può essere risolta anche
con il metodo delle forze, sopprimendo un solo grado di vincolo (interno o
esterno) per renderla
isostatica e assumendo come incognita iperstatica,
X, la reazione vincolare del vincolo
soppresso (struttura principale). Scegliendo di sopprimere un grado di vincolo esterno, si può eliminare il vincolo esterno in C,
che ha molteplicità di vincolo pari a 1 (Fig. 7).
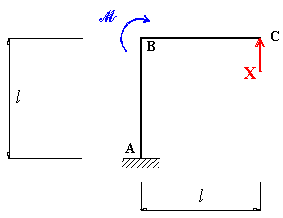
Fig. 7
Affinché la struttura di Fig. 7 possa essere considerata equivalente a quella in Fig. 1, occorre garantire che le due strutture siano sollecitate nello stesso
modo (equivalenza statica) e che ammettano le stesse componenti di spostamento
(equivalenza cinematica). Poiché, per ipotesi, X
è la reazione vincolare del carrello soppresso, l'equivalenza statica tra le due
strutture è garantita a priori. Per soddisfare anche l'equivalenza cinematica, è
sufficiente ripristinare la congruenza tra le due strutture in corrispondenza
della sezione di svincolamento. Poiché in Fig. 1 lo spostamento
verticale di C è impedito dal vincolo carrello, l'effetto
combinato della forza
X (incognita iperstatica) e della coppia
esterna
 sulla struttura principale deve produrre uno
spostamento verticale nullo del nodo C:
sulla struttura principale deve produrre uno
spostamento verticale nullo del nodo C:
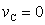 .
.
Per determinare lo spostamento verticale in C, si può utilizzare il
principio di sovrapposizione degli effetti: lo spostamento conseguente
all’azione combinata della coppia
 e della reazione vincolare incognita
X è uguale alla somma
degli spostamenti conseguenti a
e della reazione vincolare incognita
X è uguale alla somma
degli spostamenti conseguenti a
 e
X, nell'ipotesi che
e
X, nell'ipotesi che
 e
X agiscono separatamente sulla struttura. In quanto segue, si assumono positivi
gli spostamenti verticali verso il basso e positive le rotazioni orarie.
e
X agiscono separatamente sulla struttura. In quanto segue, si assumono positivi
gli spostamenti verticali verso il basso e positive le rotazioni orarie.
Anche quando si decide di risolvere un telaio a nodi spostabili con un
metodo diverso da quello dei telai a nodi spostabili, bisogna
sempre prestare molta
attenzione a non trascurare le componenti indipendenti di spostamento nodale
nelle equazioni risolventi. In sostanza, qualunque sia il metodo solutivo
prescelto, la soluzione non può in alcun caso prescindere dalle componenti
indipendenti di spostamento nodale. Infatti, anche se la struttura su cui
opera il metodo delle forze è isostatica, la travatura reticolare associata al
telaio è comunque labile. Di conseguenza, nel telaio sono sicuramente
presenti tante componenti indipendenti di spostamento nodale quanti sono i gradi
di libertà della travatura reticolare associata. Nel nostro caso, la componente
indipendente di spostamento nodale è solo una, lo spostamento orizzontale dei
nodi B e C.
Valutiamo
vC
facendo uso della composizione cinematica delle rotazioni e degli spostamenti.
Con riferimento alla Fig. 8,
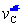 ,
spostamento verticale del nodo C quando sulla struttura è presente la
sola coppia concentrata
,
spostamento verticale del nodo C quando sulla struttura è presente la
sola coppia concentrata
 ,
risulta dalle seguenti relazioni:
,
risulta dalle seguenti relazioni:

Fig. 8
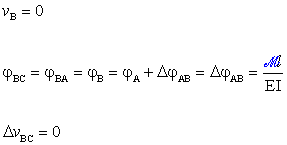
da cui segue:
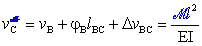 .
(per ulteriori dettagli sul calcolo di
.
(per ulteriori dettagli sul calcolo di
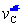 ,
clicca qui)
,
clicca qui)
Analogamente per
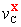 ,
spostamento verticale in C dovuto alla sola incognita iperstatica
X, si ricava (Fig. 9):
,
spostamento verticale in C dovuto alla sola incognita iperstatica
X, si ricava (Fig. 9):
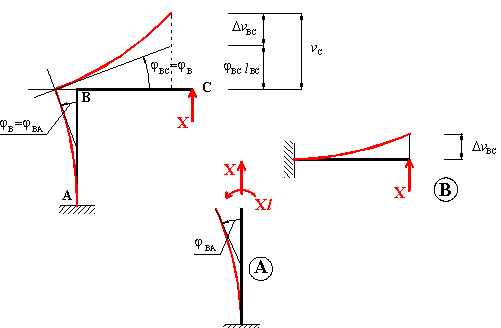
Fig. 9
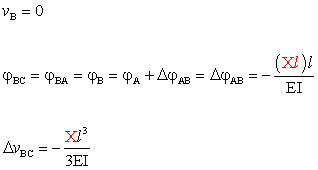
da cui:
 .
(per ulteriori dettagli sul calcolo di
.
(per ulteriori dettagli sul calcolo di
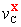 ,
clicca qui)
,
clicca qui)
Per il principio di sovrapposizione degli effetti, si può porre:
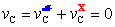
da cui, sostituendo i valori di
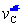 e
e
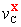 ,
si ricava il modulo dell'incognita iperstatica
X:
,
si ricava il modulo dell'incognita iperstatica
X:
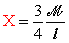 .
.
Verifichiamo che la reazione vincolare VC del carrello in Fig.
1 sia effettivamente uguale all'incognita
X
appena ricavata.
Per l’equilibrio alla rotazione dell’asta BC rispetto al punto B di
Fig. 10, ottenuta suddividendo il telaio in travi semplicemente appoggiate, caricate
dalle azioni esterne e dai momenti della soluzione iperstatica, si ha:
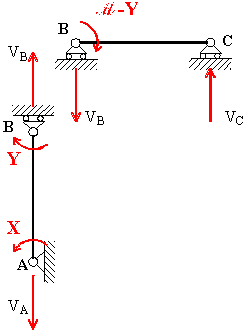
Fig. 10
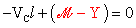
da cui, sostituendo a
Y il suo valore,
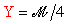 ,
si ottiene:
,
si ottiene:
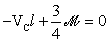
ovvero:
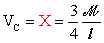 .
cvd
.
cvd
Avendo ricavato VC con segno positivo, la
reazione vincolare VC ha il verso
ipotizzato in Fig. 10, ovvero, è diretta verso l'alto (come
X). Infatti, per l'equilibrio alla rotazione
di BC le due reazioni vincolari VB
e VC devono costituire una coppia
di ugual momento e verso opposto rispetto alla coppia oraria che insiste sul
nodo B.
Un altro possibile svincolamento per rendere la struttura isostatica è quello
che consiste nel togliere un grado di vincolo interno, per esempio, inserendo una cerniera nel nodo B (Fig. 11).
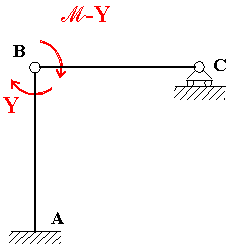
Fig. 11
La cerniera inserita in B attiva la rotazione relativa tra i tronchi AB e
BC (impedita prima dello svincolamento). Per ripristinare la congruenza
angolare in B si deve imporre che la rotazione relativa in B sia
nulla anche dopo lo svincolamento:
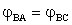 .
.
Anche
in questo caso,
bisogna prestare
molta attenzione a non trascurare le componenti indipendenti di spostamento
nodale nelle equazioni risolventi (una equazione di congruenza).
Per calcolare la
rotazione jBC,
si può far uso dello schema appoggio-appoggio con coppia concentrata su uno
degli appoggi, perché il tronco BC è appoggiato in
B e C (Fig. 11):
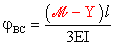 .
.
Per calcolare la rotazione
jBA,
invece, si può osservare che, poiché
il nodo B è
libero di spostarsi orizzontalmente per la presenza di un grado di libertà allo
spostamento orizzontale, il tronco BA è una trave a mensola incastrata in A
con estremo libero in B (Fig. 11):
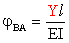 .
.
è della
massima importanza osservare che, adottando uno schema appoggio-appoggio anche
per il tronco BA, si sarebbe trascurato il contributo alla rotazione in B
conseguente alla componente indipendente di spostamento orizzontale
d. In tal caso, il telaio sarebbe stato
erroneamente risolto come telaio a nodi fissi.
Uguagliando le due rotazioni jBC
e
jBA,
si ricava:
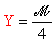 .
.
A differenza del metodo dei telai a
nodi spostabili, il
metodo delle forze non fornisce, in soluzione, lo spostamento orizzontale del nodo
B. Per determinare
d,
si può considerare, ancora una volta, il comportamento a mensola dell’asta AB
incastrata in A, con una coppia in B di momento
Y pari a
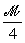 :
:
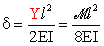 .
.
Risoluzione dei telai a nodi spostabili con il metodo
dei vincoli ausiliari
Con il
metodo dei vincoli ausiliari, la soluzione
del telaio a nodi spostabili viene perseguita in due fasi distinte, per
scomporre il problema nella somma di due problemi di più agevole soluzione.
Nella fase 1,
si bloccano tutte le componenti di traslazione dei nodi tramite vincoli
ausiliari, risolvendo
il telaio a nodi fissi che ne deriva.
I vincoli ausiliari sono vincoli fittizi che, tramite le loro reazioni
vincolari, imprimono alla struttura delle forze supplementari, non presenti sul
telaio originario. Nella fase 2, i vincoli ausiliari vengono
rimossi e alla struttura (privata del carico esterno) vengono applicate le
reazioni vincolari ausiliarie con verso opposto.
Applicando il metodo al telaio in Fig. 1, reso isostatico per
mezzo di uno svincolamento alla rotazione in B,
impediamo lo spostamento orizzontale di BC tramite un
carrello ad asse di scorrimento verticale posto in C (fig. 12).

Fig. 12
Come mostrato nel dettaglio di
Fig. 12, per l'introduzione
del vincolo ausiliario in C che blocca la traslazione orizzontale di BC,
l’asta AB diventa una mensola incastro-appoggio con coppia concentrata
sull'appoggio. La rotazione in B
dell'asta AB per effetto della coppia Y
(rotazione di fase 1) si ottiene dalla soluzione dello schema iperstatico
incastro-appoggio:
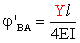 .
.
Sempre
dalla soluzione
dello schema iperstatico incastro-appoggio, si ricava anche la reazione
vincolare del vincolo ausiliario:
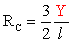 .
.
Per calcolare la
rotazione
jBC
di fase 1, si può far uso dello schema appoggio-appoggio con coppia concentrata
su uno degli appoggi, perché l’asta BC è appoggiata in
B e C:
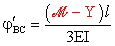 .
.
Passando alla fase 2,
si deve togliere il vincolo
ausiliario e applicare in C
la reazione del carrello ausiliario cambiata di verso. Poiché nella fase 2 il
tratto BC può traslare orizzontalmente, la reazione vincolare RC,
cambiata di verso, imprime uno spostamento orizzontale e un'ulteriore rotazione al nodo B
dell'asta AB (rotazione di fase 2).
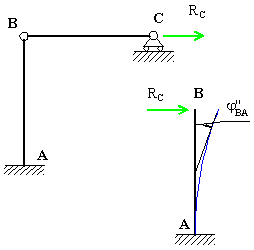
Fig. 13
Nell'ipotesi di poter trascurare la deformabilità assiale di
BC, lo spostamento orizzontale impresso al nodo B dalla reazione
vincolare ausiliaria cambiata di verso è uguale allo spostamento orizzontale
impresso al nodo C. Tale spostamento può essere valutato sullo schema a
mensola con forza concentrata
all'estremo libero, riportato nel dettaglio di Fig. 13.
I versi di RC
in Fig. 12 e 13 sono i versi effettivi. Dunque, la rotazione jBC
di fase 2 è ancora una rotazione oraria, di valore:
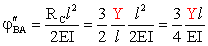 .
.
Per quanto riguarda jBC,
invece, non si hanno ulteriori contributi alla rotazione di fase 2, in quanto BC
può solo traslare rigidamente:
 .
.
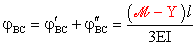 .
.
Test di verifica dell'apprendimento:
