| Prodotto scalare |
Il prodotto scalare, o prodotto interno, tra due vettori v1 e v2 è una operazione che si indica con:
![]()
oppure con
![]()
e si legge "v1 scalare v2".
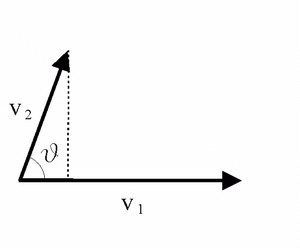
Il risultato dell'operazione è uno scalare, definito dal prodotto tra i moduli dei vettori v1 e v2, moltiplicato per il coseno dell'angolo compreso tra i due vettori (v. figura):
![]()
dove il termine v2 cosJ rappresenta il modulo della proiezione ortogonale di v2 su v1.
Poiché il risultato dell'operazione v1 · v2 è uno scalare che si ottiene come prodotto di quantità scalari, la proprietà commutativa del prodotto tra scalari si estende al prodotto scalare tra vettori:
![]()
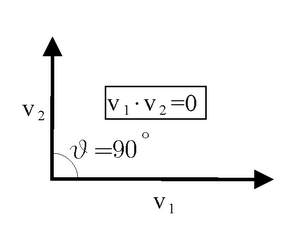
Essendo cos(π/2)=0 e cos(0)=1, il prodotto scalare si annulla se i vettori v1 e v2 sono ortogonali e assume il massimo tra tutti i valori possibili quando i vettori v1 e v2 sono paralleli.
Se i vettori sono dati in componenti cartesiane, il prodotto scalare si esprime come somma dei prodotti delle componenti omologhe, cioè relative allo stesso asse del sistema di riferimento. Dunque, dati i due vettori dello spazio v1 ≡ (v1x, v1y, v1z) e v2 ≡ (v2x, v2y, v2z) rispetto ad un sistema di riferimento cartesiano ortogonale (O, x, y, z), si ricava:
![]()
Analogamente, se v1 ≡ (v1x, v1y) e v2 ≡ (v2x, v2y) sono vettori del piano, rispetto agli assi del sistema di riferimento cartesiano ortogonale (O, x, y,) il prodotto scalare si esplicita come segue:
![]()