Un'operazione si dice invariantiva quando permette di trasformare un sistema di vettori, Σ, in un secondo sistema di vettori, Σ′, equivalente a Σ. In sostanza, un'operazione invariantiva consiste nell'aggiungere al sistema dato un sistema equivalente a zero. è possibile, per esempio:

• sostituire un vettore v applicato in P con due vettori applicati in P, la cui risultante sia v;

• sostituire due vettori applicati in P con la loro risultante applicata in P;

• aggiungere al sistema di vettori dato una coppia a braccio nullo;

ottenendo, in ogni caso, un sistema di vettori equivalente al sistema dato.

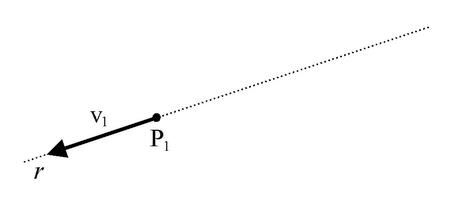
    Combinando la seconda e la terza operazione invariantiva, è possibile definire una nuova operazione invariantiva. Si consideri il sistema di vettori costituito dal solo vettore v₁, con punto di applicazione P₁ e retta d'azione r. 

Fig. 1

    Si aggiunga al sistema una coppia a braccio nullo (terza operazione invariantiva), costituita dal vettore v₂, opposto a v₁ e applicato in P₁, e dal vettore v₃, equipollente a v₁ e applicato in P₂, un punto della retta r diverso da P₁. Avendo fatto uso di un'operazione invariantiva, il sistema in Fig. 1 risulta equivalente al sistema di vettori in Fig. 2, costituito dai vettori v₁, v₂ e v₃.  

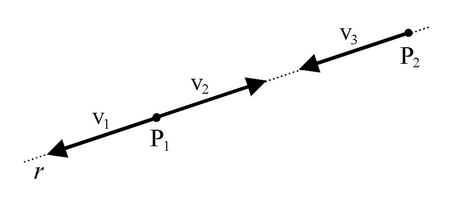
Fig. 2

    I vettori v₁ e v₂ costituiscono un sistema equivalente a zero. Sostituendo ad essi la loro risultante (seconda operazione invariantiva), ovvero, il vettore nullo, il sistema di partenza risulta equivalente al sistema formato dal solo vettore v₃. In conclusione, il vettore v₁ è equivalente al vettore v₃, traslato di v₁ nel punto P₂. 

è equivalente a

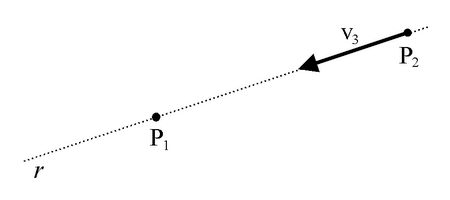
Fig. 3

    Dunque, l'operazione di traslazione di un vettore lungo la propria retta d'azione è un'operazione invariantiva.

    Combinando la prima e la terza operazione invariantiva, si ottiene un'ulteriore operazione invariantiva. Sempre con riferimento al vettore v₁ applicato in P₁, si consideri un punto P₃ non appartenente alla retta d'azione di v₁. Tale punto può sempre essere pensato come punto di applicazione di un vettore nullo.

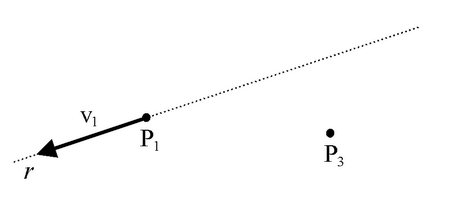
Fig. 4

    Per la prima operazione invariantiva, è possibile sostituire al vettore nullo un sistema equivalente a zero. Tra tutti i possibili sistemi equivalenti a zero, si consideri quello costituito dai due vettori v₂ e v₃, con v₂ opposto a v₁ e v₃ equipollente a v₁. Per quanto detto, il sistema di vettori v₁, v₂, v₃ è equivalente al solo vettore v₁.

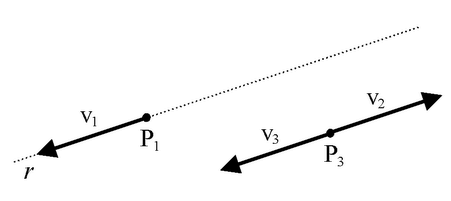
Fig. 5

    Poiché i vettori v₁ e v₂ costituiscono una coppia di momento uguale al momento di v₁ rispetto a P₃ (momento di trasporto) e il vettore v₃ può essere visto come trasporto parallelo del vettore v₁ nel punto P₃, si può concludere che è lecito traslare un vettore parallelamente a se stesso purché si aggiunga il momento di trasporto.

è equivalente a

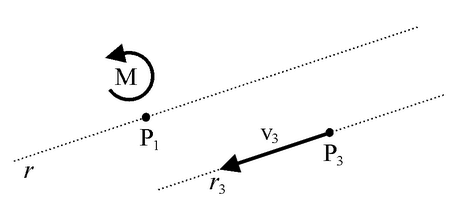
Fig. 6

Test di verifica dell'apprendimento:

Risultante tra coppie e forze concentrate

Risultante tra forze incidenti

Risultante tra forze parallele

Argomenti correlati:

Coppia, sistemi equivalenti di vettori, sistemi equivalenti a zero, vettore, vettore applicato, vettore risultante, vettori equipollenti.