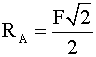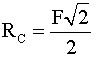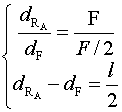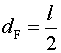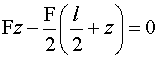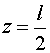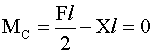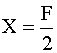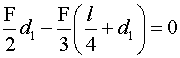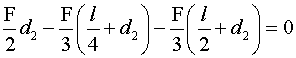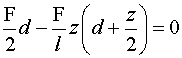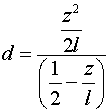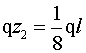Generalità
La curva delle pressioni prende anche il nome di
poligono delle pressioni o
luogo delle successive risultanti. In breve, si indica con c.d.p.
La denominazione "luogo delle successive risultanti"
deriva dal fatto che la curva delle pressioni può essere
definita
come luogo delle rette d'azione delle successive risultanti, intendendo per
successive risultanti la successione di vettori che un ideale osservatore ricaverebbe
se calcolasse la
risultante di tutte le forze incontrate nel percorrere l'asse geometrico
della struttura a partire da un suo estremo, man mano che al sistema di forze già "viste"
si aggiunge una nuova forza. Ogni lato del poligono è associato ad un tratto di
struttura compreso tra i punti di applicazione di due forze consecutive, che
possono essere forze esterne o reazioni vincolari, e rappresenta la
retta
d'azione della risultante di tutte le forze che precedono il tratto di struttura cui è associato.
Se sulla struttura sono presenti carichi distribuiti, il poligono delle pressioni può anche avere tratti curvi. In ogni
caso, la curva delle pressioni va sempre ricercata
applicando la definizione,
ovvero, immaginando di percorrere la struttura a partire da un suo estremo e
calcolando la risultante delle forze che si incontrano via via. In ultima
analisi, dunque, il problema della costruzione della curva delle pressioni si
risolve in un problema di ricerca della risultante di un
sistema di forze.
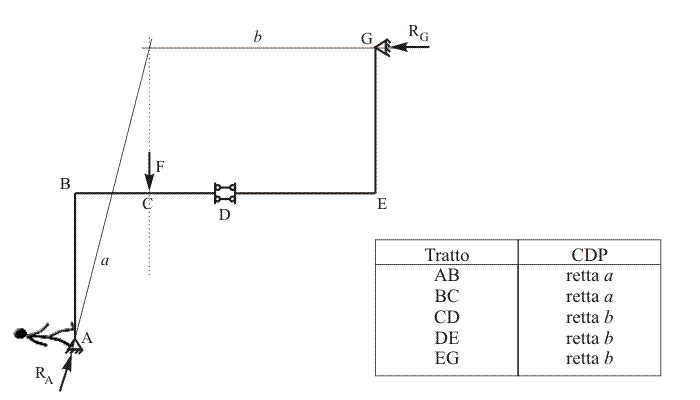
Per comprendere meglio come venga stabilita l'associazione
tra tratti di struttura e lati del poligono, passa col mouse sull'asse
geometrico della struttura riportata qui sotto, muovendoti dal nodo A al nodo G
e tenendo presente che l'osservatore riportato in
figura
coincide con la sezione di riferimento per il calcolo della risultante delle
forze che precedono.
La costruzione della curva delle pressioni è indipendente
dall'estremo della struttura scelto come origine. Infatti, per l'equilibrio
della struttura, i due sistemi di forze che precedono e che seguono una
determinata sezione devono farsi equilibrio, nel senso che la risultante del
sistema di forze che precedono la sezione è una forza direttamente opposta (e quindi equilibrante) alla risultante
del sistema di forze che si trovano oltre la sezione. Dunque, le rette d'azione delle due risultanti coincidono e
l'osservatore che arriva in una determinata sezione calcola una risultante che è
applicata sempre lungo la stessa retta, sia che egli giunga da destra o da
sinistra. A cambiare in funzione della direzione secondo la quale si muove
l'osservatore è solo il verso della risultante delle forze "viste"
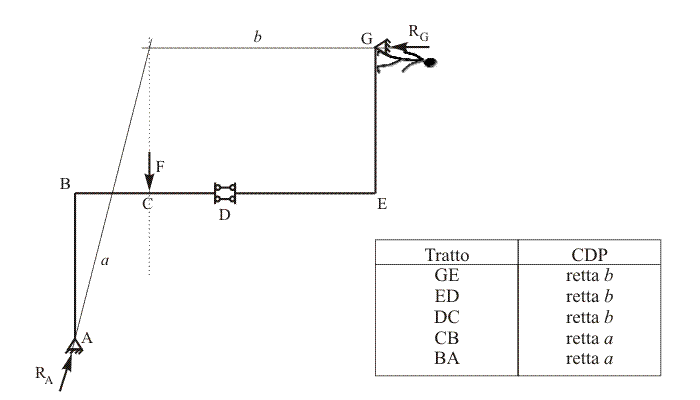
dall'osservatore. A chiarimento di quanto affermato, passa col mouse sull'asse
geometrico della struttura riportata qui sotto, muovendoti dal nodo G al nodo A,
e confronta i risultati con quelli ricavati nel caso precedente.
Definita la curva delle pressioni per tutti i tratti della
struttura, la risultante di tutte le forze che precedono una determinata sezione
è la forza, somma vettoriale delle forze che precedono la sezione, applicata nel
punto del corrispondente tratto della curva delle pressioni che si trova sulla
normale alla struttura condotta a partire dalla sezione in esame (v. figura).
In vista delle applicazioni, facciamo alcune considerazioni
preliminari su qualche struttura elementare.
La trave appoggiata con forza in mezzeria
e vincoli inclinati a 45°
Ricaviamo la curva delle pressioni per la trave appoggio-appoggio caricata nel
suo punto medio B
(v. figura), ricordando anche i passi fondamentali che conducono alla
determinazione delle reazioni vincolari per via grafica.
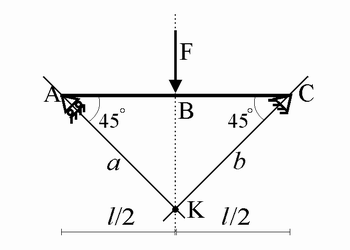
La struttura in esame è soggetta a sole tre forze: le due reazioni vincolari e
la forza esterna. Di queste tre forze, conosciamo la retta d'azione del vincolo
carrello, ortogonale al piano di scorrimento del vincolo e passante per il
vincolo stesso, e la retta d'azione, l'intensità e il verso della forza esterna
(assegnati dal problema). La retta d'azione del vincolo carrello incontra quella
della forza esterna nel punto K. Sappiamo, inoltre, che la cerniera C può
reagire con una forza RC applicata in C e comunque
diretta nel piano.
Poiché si suppone che la trave sia in equilibrio, il sistema di forze costituito
dalla forza esterna e dalle reazioni vincolari deve essere
equivalente a zero.
In base al Teorema
N, condizione necessaria (e in generale non sufficiente) affinché un sistema
di tre forze applicate ad un corpo rigido sia equivalente a zero è che le forze
siano complanari e concorrenti in uno stesso punto, proprio o
improprio
(condizione necessaria di equivalenza a zero). Dunque, le rette d'azione della
forza esterna e delle reazioni vincolari
devono incontrarsi in uno stresso punto. Ne segue che la reazione della cerniera
C avrà retta d'azione passante per K, oltre che per C.
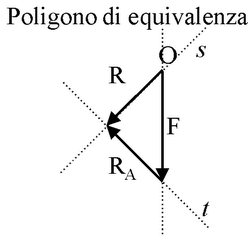
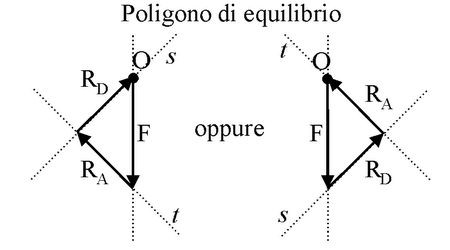
Determinate tutte le rette d'azione, è possibile costruire il poligono di
equilibrio che, in questo caso, essendo solo tre le forze da equilibrare, è un triangolo di equilibrio: a partire da un punto O del piano, scelto a piacere,
si riporta un vettore
equipollente alla forza esterna F. Convenendo di riportare sul
triangolo di equilibrio i moduli dei vettori, e non i vettori, il vettore
applicato in O equipollente a F è stato indicato in figura con la
lettera F, modulo di F. Dal punto di applicazione O
e dall'estremo di questo vettore, si tracciano due rette, t e s, parallele alle rette
d'azione delle reazioni vincolari, a e b. Per la proprietà commutativa di cui gode la
somma vettoriale, detta t la retta parallela alla reazione vincolare del
carrello e s la retta parallela alla reazione vincolare della cerniera,
le costruzioni grafiche possibili per il triangolo di equilibrio sono due, del tutto equivalenti tra loro.
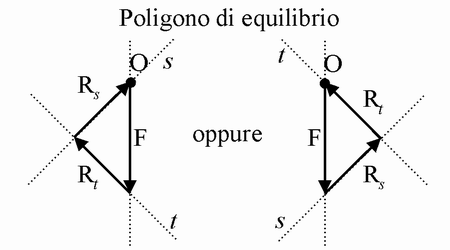
I lati del triangolo di equilibrio distesi lungo le rette t e s possono
essere usati per definire in direzione e modulo due vettori, che chiameremo,
rispettivamente, Rt e Rs.
Fissando i versi di questi due vettori in modo che la
somma vettoriale di F, Rt
e Rs sia un
vettore nullo (v. figura),
il sistema di tre forze composto dal vettore applicato in O equipollente a
F, Rt e Rs
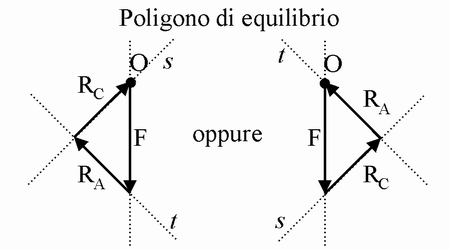
soddisfa la prima equazione cardinale della statica. Inoltre, detti RA e RC,
rispettivamente, i vettori con rette d'azione a e b equipollenti a Rt
e Rs, anche il sistema di tre forze formato da
F, RA e RC
soddisfa la prima equazione cardinale della statica. Va ricordato che, in
generale, la chiusura del poligono delle forze non è condizione sufficiente per
soddisfare anche la seconda equazione cardinale della statica, nel senso che non
è sufficiente ad escludere l'eventualità che il sistema di forze possa essere
equivalente ad una coppia. La chiusura del poligono di tre forze diventa
condizione sufficiente per soddisfare anche la seconda equazione cardinale della
statica solo se le rette d'azione delle tre forze concorrono in uno stesso
punto, soddisfacendo la condizione necessaria di equivalenza a zero. In queste
ipotesi, il sistema di tre forze risulta essere equivalente a zero e i vettori RA
e RC, di modulo, direzione e verso definiti dalla
chiusura del triangolo di equilibrio, rappresentano le due reazioni vincolari in
A e C.
Per la consuetudine di riportare sul triangolo di equilibrio
soli i moduli dei vettori,
è possibile indicare i vettori distesi lungo le rette t e s del
triangolo di equilibrio con RA e RC, moduli di RA e RC,
restando inteso che essi non rappresentano le effettive reazioni vincolari RA
e RC, ma due vettori ad esse equipollenti, la cui
posizione nel piano è legata alla scelta arbitraria del punto O fra gli
∞² punti del piano.
Poiché il triangolo di equilibrio per la struttura in questione è un triangolo rettangolo isoscele,
si ricava:
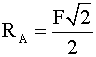
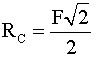
Passando ora alla costruzione della curva delle pressioni, si consideri di
percorrere la struttura dall'estremo A all'estremo C. Per prima cosa, dobbiamo
definire i tratti della struttura a cui associare i lati del poligono delle
pressioni. Per definizione di curva delle pressioni, ogni tratto
in cui viene suddivisa la struttura
deve essere compreso tra i punti di applicazione di due forze consecutive, siano
esse forze esterne o reazioni vincolari. Ne segue che i tratti da considerare
in questo caso sono solo due: i tratti AB e BC.
Partendo dal nodo A, il
nostro osservatore virtuale incontra subito la reazione vincolare
RA. Dunque, la retta d'azione di
RA sarà curva delle pressioni finché l'osservatore non
incontra una nuova forza, ovvero, finché non arriva nel punto B. In conclusione,
a, retta d'azione di
RA, è il lato della curva delle pressioni associato al tratto AB.
Giunto in B, il problema che si presenta al nostro osservatore è quello di
determinare la risultante tra la reazione vincolare
RA e la forza esterna F. Si tratta di
ricavare la risultante
di due forze incidenti, problema affrontato in apposita
scheda. D'altra parte, la risultante cercata
dall'osservatore è a lui già nota. Infatti, ricordando che, per l'equilibrio della
struttura, le forze che precedono una sezione devono fare equilibrio alle forze
che seguono quella stessa sezione, la risultante tra
RA e F deve essere una forza uguale e
opposta all'unica forza che si trova oltre il punto B, la reazione vincolare
RC. In particolare, è già nota la retta d'azione della
risultante tra
RA e F, che è b, la retta d'azione di
RC. Dunque, la curva delle pressioni per il tratto BC è la
retta b.
La curva delle pressioni per il tratto BC può essere ricavata anche sfruttando
il metodo testa-coda per la determinazione della risultante di un sistema di
forze. Infatti, disponendo in successione, a partire da un punto O del piano
scelto a piacere, le due forze di cui si vuole ricavare
la risultante,
RA e F, si ottiene un secondo triangolo,
detto triangolo di equivalenza, identico al triangolo di equilibrio salvo per il
verso di orientazione dell'ultimo lato.
Dal confronto tra il triangolo di equilibrio e il triangolo di equivalenza, è possibile verificare che R,
risultante di
RA e F, è, effettivamente, una forza uguale
e opposta a
RC, l'unica forza che si trova oltre il punto B. Per quanto
riguarda la retta d'azione di R, sappiamo che essa deve passare
per il punto K (v.
scheda). Essendo poi la retta d'azione di R
parallela alla retta d'azione di
RC, essa coincide con la retta b.
Si vuole qui sottolineare che, per retta d'azione di
R, si intende la retta d'azione della risultante R
delle due forze
RA e F incidenti sulla struttura ABC e non
retta d'azione del suo vettore equipollente che compare nel
triangolo di equivalenza. Per l'arbitrarietà del punto O del piano, infatti, le
rette d'azione definibili per il vettore equipollente a R
sono ∞², essendo ∞² i punti del piano.
I risultati ottenuti sono sintetizzati nella seguente tabella, che completa la
soluzione del problema della determinazione della curva delle pressioni per la
trave ABC:
|
Tratto |
Curva delle pressioni |
|
AB
BC |
retta a
retta b |
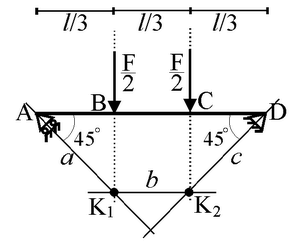
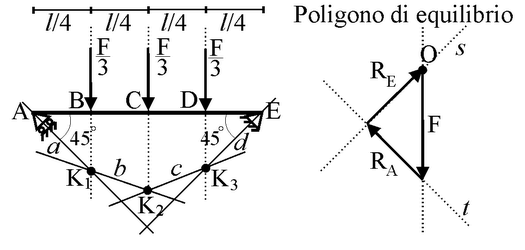
La trave appoggiata con due forze concentrate simmetriche e vincoli inclinati a 45°
Ci proponiamo ora di ricavare la curva delle pressioni per la trave con due
forze concentrate, simmetriche rispetto alla mezzeria, mostrata in figura:
Ai fini della determinazione delle reazioni vincolari, è lecito sostituire le
due forze esterne con la loro risultante, in quanto si tratta di un'operazione
invariantiva. Poiché la risultante di due forze
concordi è interna alle due forze, ha modulo pari alla somma dei moduli e dista
dalle due forze per quantità che sono inversamente proporzionali all'intensità
delle forze stesse (v. scheda),
la risultante delle forze esterne è una forza
identica a quella dell'esempio precedente, ancora applicata in mezzeria. Di
conseguenza, per la determinazione delle reazioni vincolari si ricade nel caso precedente,
nel senso che esse sono
identiche a quelle calcolate per la trave caricata in mezzeria. Anche il
poligono di equilibrio è identico a quello del caso precedente, se viene
costruito usando la
risultante delle due forze esterne.
Volendo ora ricavare la curva delle pressioni, definiamo i tratti di struttura
di interesse. In questo caso, i tratti di struttura lungo i quali rimane costante la
risultante delle forze sono tre: AB, BC e CD.
Tra A e B, l'osservatore virtuale deve trovare la risultante di un sistema
formato da un'unica forza, la reazione vincolare
RA. Quindi, la curva delle pressioni per il tratto AB
coincide con la retta d'azione di
RA, la retta a.
In B, l'osservatore incontra la prima forza concentrata di intensità F/2, che
deve comporre vettorialmente con
RA. Sappiamo che la risultante di
RA e F/2 deve passare per il punto K1,
intersezione delle rispettive rette d'azione (v.
scheda). Inoltre, sappiamo che la risultante di tutte
le forze che precedono la generica sezione del tratto BC deve essere uguale e
opposta alla risultante delle forze che seguono la sezione stessa. Oltre il
tratto BC, sono presenti solo due forze, l'altra forza concentrata e
RD. La loro risultante deve passare per il loro punto di
intersezione, K2. Ci troviamo quindi di fronte a due forze, una
applicata in K1 e una applicata in K2, che devono farsi
equilibrio. Perché ciò avvenga, le due forze devono essere direttamente opposte,
ovvero, devono avere stesso modulo ed essere applicate lungo la stessa retta
d'azione. Di conseguenza, la risultante di
RA e F/2 passa per entrambi i punti K1
e K2 (retta b).
Per il tratto CD, l'osservatore deve calcolare la risultante di
RA, F/2 applicata in B e F/2
applicata in C. Come osservato in precedenza, questa risultante deve essere
uguale e opposta all'unica forza che si trova oltre il punto C. Dunque, la sua
retta d'azione è c, retta d'azione di
RD.
In conclusione, la curva delle pressioni è fornita, tratto per tratto, dalla
seguente tabella riassuntiva:
|
Tratto |
Curva delle pressioni |
|
AB
BC
CD |
retta a
retta b
retta c |
Osserviamo, a questo punto, che la curva delle pressioni per in tratto BC può
essere ottenuta direttamente dal poligono di equilibrio, ricordando che la forza
F è la risultante delle due forze concentrate di intensità F/2.
Dunque, la forza F può essere sostituita dalle due forze F/2
poste in successione (operazione invariantiva):
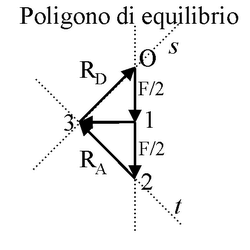
La somma vettoriale tra
RA e la forza concentrata F/2 applicata in B
può essere letta sul poligono di equilibrio come risultante dei vettori (2-1) e
(3-2), ove si è fatto uso della convenzione di Grassmann. La risultante dei
vettori (2-1) e (3-2) è il vettore (3-1), che ha direzione orizzontale. La retta d'azione
della risultante tra
RA e la forza concentrata F/2 applicata in B, dovendo essere orizzontale e
dovendo passare per K1, è la retta b.
La trave appoggiata con tre forze concentrate simmetriche e vincoli inclinati a 45°
Estendiamo i risultati dell'esercizio precedente per definire la curva delle
pressioni nella trave appoggiata con tre forze concentrate facendo uso del poligono delle forze. Come prima, ai fini della
determinazione delle reazioni vincolari è lecito sostituire le forze esterne con
la loro risultante, F. Poligono d'equilibrio e reazioni vincolari, quindi, sono
identici a quelli dell'esercizio precedente.
A questo punto, dividiamo la forza F del poligono d'equilibrio in
tre parti uguali, operazione lecita in quanto operazione invariantiva.
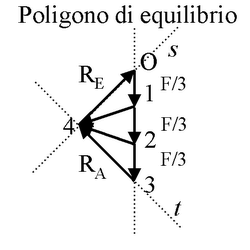
Per quanto osservato in precedenza, la curva delle pressioni per il tratto BC è
parallela al vettore (4-2) e passa per K1, punto d'intersezione
di
RA e della forza F/3 applicata in B (retta
b). La curva delle pressioni per il tratto successivo si ottiene dal
poligono componendo il vettore (4-3) con due vettori di intensità F/3, i
vettori (2-1) e (3-2), ottenendo il vettore (4-1). La retta
parallela al vettore (4-1) e passante per K2, punto
d'intersezione di b e della forza F/3 applicata in C, è la
curva delle pressioni per il tratto CD. Infine, nei tratti AB e DE la curva
delle pressioni è data dalle rette d'azione delle reazioni vincolari, come nei
casi precedenti.
In conclusione, si ottiene quanto segue:
|
Tratto |
Curva delle pressioni |
|
AB
BC
CD
DE |
retta a
retta b
retta c retta
d |
La trave appoggiata con carico distribuito e vincoli inclinati a 45°
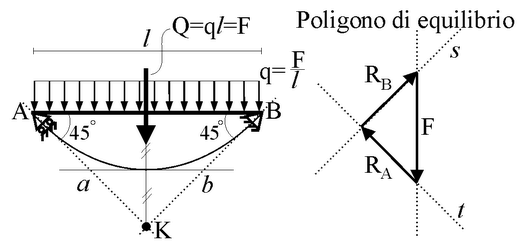
Poiché la risultante delle forze esterne è ancora una forza verticale verso il
basso di modulo F, le reazioni vincolari sono identiche a
quelle dei casi precedenti. La curva delle pressioni può essere dedotta dai casi
precedenti, considerando il carico distribuito come caso limite, ottenuto
suddividendo la forza esterna F in infinite forze infinitesime di ugual modulo,
uniformemente distribuite sulla trave.
Confrontando tra loro i casi precedenti,
ci si può rendere conto del fatto che i lati del poligono delle pressioni aumentano
all'aumentare del numero di suddivisioni della forza esterna. Al limite, per
suddivisione infinita del carico, si ottiene una parabola che è tangente in A e
B alle rette d'azione delle reazioni vincolari. La parabola può essere
considerata come poligono a infiniti lati di dimensione infinitesima. Ogni lato
infinitesimo (un
punto della parabola) è disteso lungo la retta d'azione della risultante delle
forze che precedono la sezione di cui il lato è proiezione ortogonale sulla
parabola, secondo una retta ortogonale all'asse della trave. Considerando l'osservatore
nella posizione identificata dall'ascissa corrente z, il carico
distribuito "visto" dall'osservatore ha risultante verticale di modulo qz
e passa per il baricentro del rettangolo di base z e altezza q
(v. figura).

Dal poligono d'equilibrio, possiamo ricavare la risultante tra
RA e qz in direzione modulo e verso. Ebbene,
la tangente alla parabola nel punto che si trova sulla normale all'asse della
struttura che passa per l'osservatore è parallela alla retta d'azione della risultante calcolata sul
poligono d'equilibrio. Per le proprietà geometriche che caratterizzano la
parabola, tale tangente passa per il punto Kz, intersezione
della retta a con la retta d'azione della risultante del carico
distribuito "percorso", qz. Dunque, la tangente alla parabola in
z è la retta d'azione della risultante delle forze che precedono la
sezione z. Si può anche dire che la parabola è l'inviluppo
delle rette d'azione delle successive risultanti.
Per quanto riguarda la costruzione
grafica del tratto parabolico di tangente iniziale a e tangente finale
b, si faccia riferimento all'apposita
scheda.
La trave appoggiata con forza in mezzeria
e vincoli verticali
Consideriamo ora la seguente trave appoggiata con forza concentrata in mezzeria
e vincoli ad asse verticale.

Volendo risolvere la trave per via grafica, ovvero, facendo uso del poligono di
equilibrio, dobbiamo innanzitutto determinare la direzione delle rette d'azione
delle forze che devono farsi equilibrio. Le direzioni della forza esterna e
della reazione del vincolo in A, sono note: la prima perché assegnata dal
problema e la seconda per condizione di vincolo. Poiché queste due forze sono
entrambe verticali, la loro risultante è ancora una forza verticale. Inoltre,
poiché le due forze sono discordi, la loro risultante è esterna alle due forze e
posta dalla parte della forza maggiore (v.
scheda). Noi non sappiamo ancora quale delle due
sia la forza maggiore, perché non conosciamo il modulo di
RA. Però, sappiamo che, per l'equilibrio della trave, la
risultante tra
RA e F deve essere una forza uguale e
opposta all'unica altra forza che insiste sulla trave, la reazione vincolare
della cerniera C. Di conseguenza, la risultante tra
RA e F deve essere applicata lungo la
stessa retta d'azione di RC. Poiché la cerniera C può reagire con una forza RC
applicata in C, anche la risultante di
RA e F dovrà
passare per il punto C. Dovendo poi essere una forza verticale, la sua retta
d'azione è la retta verticale per C, b.
Siamo così giunti alla definizione della curva delle
pressioni, senza dover risolvere la trave in termini di reazioni vincolari
esterne:
|
Tratto |
Curva delle pressioni |
|
AB
BC |
retta a
retta b
|
Volendo ricavare anche le reazioni vincolari, ci si può subito rendere conto del
fatto che la soluzione per mezzo del poligono delle forze è impraticabile, in
quanto tutte le forze in gioco sono tra loro parallele e il poligono
risulterebbe degenere. Però, possiamo ragionare come segue.
-
I modo: sfruttiamo la simmetria del sistema. La trave è
geometricamente simmetrica. I vincoli in A e C non sono uguali ma, per
quanto osservato in precedenza, la cerniera in C ha solo componente di
reazione verticale e, quindi, si comporta come se fosse un carrello ad asse
verticale. Dunque, per la particolare condizione di carico considerata,
i vincoli possono essere considerati simmetrici. Infine, anche il carico è
simmetrico. Poiché a cause simmetriche corrispondono effetti, cioè reazioni
vincolari, simmetrici, possiamo concludere che le due reazioni vincolari
sono uguali in modulo e concordi. Il loro verso deve essere
discorde rispetto a quello della forza esterna, in modo da equilibrarla
(rispetto della prima equazione cardinale della statica). Dunque, RA
e RC sono dirette verso l'alto e hanno modulo pari
a F/2.
Abbiamo modo di verificare la correttezza di questo risultato? Sì, se
ricordiamo che la curva delle pressioni è già stata definita. Infatti,
avendo calcolato il modulo di RA, ora possiamo ricavare la risultante tra
RA ed F sapendo che, oltre ad essere
verticale e posta
dalla parte della forza maggiore, cioè a destra di F, deve anche distare
da RA e F per quantità inversamente
proporzionali ai rispettivi moduli. Sia r una generica retta
verticale posta a destra della forza F e siano dRA e dF le
distanze di r da RA e F,
con dRA distanza orientata dalla retta a
alla retta r e dF distanza orientata dalla retta f
alla retta r
(v. figura).
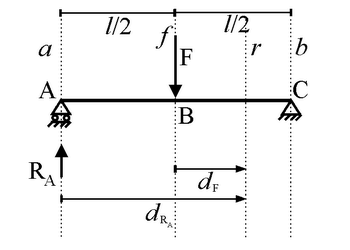
La retta r è retta d'azione della risultante che stiamo cercando per i
valori di dRA e
dF che risolvono
il seguente sistema di due equazioni nelle due incognite dRA e
dF:
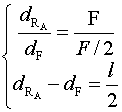
La prima equazione impone che la distanza dei punti della retta r dalle
rette a e f sia inversamente proporzionale, rispettivamente, ai
moduli delle forze RA e F, mentre la
seconda impone che, per il rispetto delle condizioni geometriche, la differenza
tra le due distanze sia pari a l/2.
Dalla prima equazione ricaviamo:
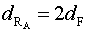
Sostituendo questo valore nella seconda equazione, si ottiene:
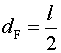
Ovvero, la risultante tra
RA e F si trova sulla retta b.
Questo risultato coincide con quanto stabilito dalla curva delle pressioni per
il tratto BC e, quindi, è corretto.
La posizione della risultante può anche essere ricavata come applicazione del
Teorema dell'asse centrale, ricordando che le forze componenti un generico
sistema di forze, Σ, hanno momento risultante nullo
rispetto a tutti i punti della retta d'azione della risultante di
Σ.
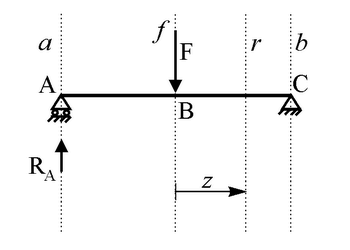
Nell'ipotesi che la risultante cercata si trovi alla destra di F,
si può definire la posizione della risultante rispetto a B tramite un'ascissa z,
di origine B e diretta verso destra (v. figura), che fissa la posizione della
retta verticale r posta a destra del punto B. La condizione di
annullamento del momento risultante del sistema di forze RA
+ F rispetto ai punti di r si esplicita come segue:
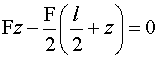
da cui segue che:
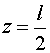
Abbiamo ottenuto nuovamente che la
risultante giace sulla retta b.
Infine, considerando la forza esterna F come somma di due forze di
modulo F/2 poste sulla stessa retta d'azione (v. figura), operazione sempre
lecita in quanto operazione invariantiva, possiamo ricondurre il
sistema di forze
RA + F al sistema ad esso equivalente
costituito da una delle due forze F/2 in mezzeria e dalla coppia
oraria di
intensità Fl/4 formata da
RA con l'altra forza F/2 in mezzeria.
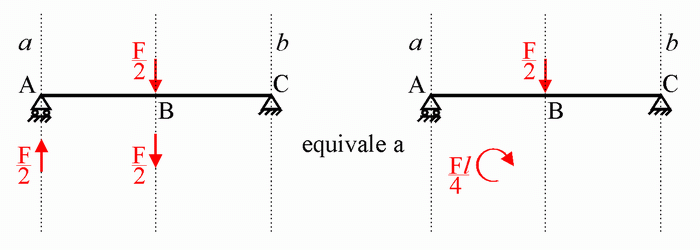
Come mostrato nella scheda dedicata alla
composizione delle forze, la
risultante di questo
sistema di forze è una forza diretta verso il basso, di modulo F/2, posta a destra del punto B e distante
da B di una quantità pari al rapporto tra il modulo della coppia e il modulo
della forza, cioè, l/2. Si è quindi ottenuta l'equilibrante di
RC, la cui retta d'azione è la retta b. Anche in
questo caso, il risultato ottenuto coincide con quanto stabilito dalla curva
delle pressioni. Possiamo anche osservare che, poiché la risultante tra
RA e F è l'equilibrante di
RC, il sistema di tre forze composto da
RA, F e
RC è equivalente a zero. Ciò significa che, per i valori di
reazione vincolare che abbiamo calcolato, la trave risulta in equilibrio.
Quindi, le reazioni vincolari calcolate sono corrette.
-
II modo: sfruttiamo la conoscenza della curva delle pressioni. Questa
volta, vogliamo calcolare il modulo di RA in modo
che la risultante tra
RA e F sia sulla retta b, come stabilito
dalla curva delle pressioni per il tratto BC. Si tratta di applicare
nuovamente il Teorema dell'asse centrale, imponendo l'annullamento del
sistema di forze
RA + F rispetto ai punti della retta b.
Detto X il modulo di
RA e assumendo che la reazione vincolare in A sia diretta
verso l'alto, la condizione di annullamento fornisce:
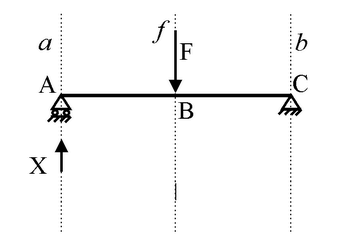
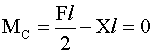
da cui si ricava:
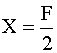
La reazione vincolare in C si determina imponendo che debba costituire,
insieme a
RA, un sistema di forze equilibrante la forza
esterna. Ne segue che anche
RC è diretta verso l'alto e ha modulo F/2.
Come verifichiamo la correttezza di questo risultato? Occorre controllare che le
reazioni vincolari ottenute soddisfino le condizioni di simmetria sul risultato
imposte dalla simmetria del sistema. Poiché le reazioni vincolari sono
simmetriche, il risultato è corretto.
-
III modo: sfruttiamo le condizioni di vincolo. Poiché in C è presente
un vincolo che non è in grado di reagire a momento flettente, il momento
risultante rispetto al punto C di tutte le forze presenti sulla trave deve
essere nullo. Le forze presenti sulla trave sono tre:
RA, F e
RC. Poiché
RC ha braccio nullo rispetto a C, è sufficiente annullare
il momento del sistema di forze
RA + F rispetto al punto C. Detto X il
modulo di
RA e assumendo che la reazione vincolare in A sia diretta
verso l'alto, l'equazione che esprime l'annullamento del momento rispetto a
C è identica a quella scritta per il II procedimento. Da questo punto in
poi, il II e III procedimento coincidono.
La trave appoggiata con due forze concentrate simmetriche e vincoli verticali

Poiché, ai fini della determinazione delle reazioni vincolari, è lecito
sostituire le forze esterne con la loro risultante,
RA e
RD sono identiche alle reazioni vincolari del caso precedente.
Per quanto riguarda la curva delle pressioni, i tratti di interesse sono AB, BC
e CD. Partendo da A, l'unica forza che si incontra è
RA fino a quando si giunge in B. Arrivati in B, dobbiamo
trovare la risultante tra
RA e la forza concentrata in B. Queste due forze costituiscono
coppia. Come mostrato nella scheda ad essa dedicata, la
risultante di una coppia è un vettore nullo
applicato sulla retta impropria. Giunti nel punto C, bisogna calcolare la
risultante tra
RA, la forza concentrata in B e la forza concentrata in C.
Per quanto più volte osservato in precedenza, tale risultante dovrà equilibrare
la reazione
RD e, quindi, avrà la sua stessa retta d'azione. In
alternativa, si può facilmente verificare che la
risultante tra la forza
concentrata in C e la coppia oraria formata da
RA con la forza concentrata in B è proprio una forza
diretta verso il basso, con retta d'azione d e modulo pari a F/2.
In conclusione, la curva delle pressioni per la struttura in esame è la
seguente:
|
Tratto |
Curva delle pressioni |
|
AB
BC
CD |
retta a
retta impropria
retta d
|
La trave appoggiata con tre forze concentrate simmetriche e vincoli verticali

Per quanto riguarda la ricerca delle reazioni vincolari, valgono le
considerazioni fatte per l'esempio precedente. Dunque
RA =
RE = F/2.
I tratti di interesse per la determinazione della curva delle pressioni sono AB,
BC, CD e DE. Nel tratto AB la curva delle pressioni è ancora la retta a.
Per il tratto BC, occorre determinare la risultante tra
RA e la forza concentrata in B. Essendo due forze
parallele, la loro risultante si trova su una retta ad esse parallela. Inoltre,
poiché le due forze hanno verso opposto, la loro risultante è esterna alle due
forze e posta dalla parte della forza di modulo maggiore, la reazione vincolare.
Calcoliamo la posizione della risultante facendo uso del Teorema dell'asse
centrale. Imponiamo, cioè, che il momento risultante del sistema costituito
dalle due forze sia nullo rispetto ai punti della retta d'azione della loro
risultante. Chiamando d1 la distanza della retta d'azione della risultante
dal punto A, orientata come in figura, dalla condizione di annullamento del momento risultante
si ottiene:
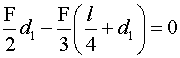
da
cui ricaviamo d1=l/2. Essendo positivo il segno di d1,
che, ricordiamo, è una distanza orientata, rimane confermata l'ipotesi iniziale
secondo la quale la risultante tra
RA e la forza concentrata in B si trova a sinistra del
punto A.
Per il tratto CD, fissiamo d2, l'ascissa che definisce la
posizione della nuova risultante, in modo che abbia stessa origine e stesso
verso di d1 e determiniamone il valore facendo nuovamente uso
del Teorema dell'asse centrale. Per il nuovo sistema di forze, costituito da
RA, la forza applicata in B e la forza applicata in C, si
ottiene:
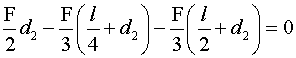
da
cui si ricava d2 = –
3/2 l. Poiché d2 ha
segno negativo, il verso assunto in prima approssimazione per d2
è errato e la nuova risultante si trova, in realtà, a destra del punto A.
Per il tratto DE, valgono le considerazioni fatte a proposito degli esempi
precedenti. In conclusione:
|
Tratto |
Curva delle pressioni |
|
AB
BC
CD DE |
retta a
retta b
retta c
retta d
|
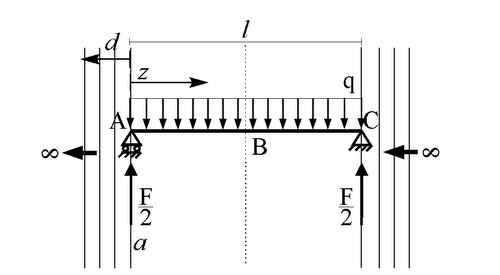
La trave appoggiata con carico distribuito e vincoli verticali
Il carico distribuito può essere trattato come caso limite dei casi precedenti,
ricavato per suddivisione della forza esterna F in infinite forze
infinitesime di ugual modulo, uniformemente distribuite sulla trave. Possiamo
osservare che il carico distribuito ha la stessa direzione delle reazioni
vincolari. Di conseguenza, quando l'osservatore si trova nella posizione
individuata dall'ascissa z, le forze che deve comporre,
RA e la risultante della quota di carico distribuito
compresa tra A e z, sono forze parallele. Pertanto, la loro risultante si
troverà sempre su una retta parallela alla retta a e la curva delle
pressioni non presenterà il ramo parabolico osservato nel caso dei vincoli
inclinati.
Occupiamoci di determinare la posizione della retta verticale su cui è applicata
la risultante delle forze "viste" dall'osservatore quando egli si trova in z,
fissando l'ascissa orientata d come in figura. La risultante del carico distribuito
"visto" dall'osservatore che si trova in z, è una forza di modulo pari
all'area del rettangolo di base z e altezza q, con q
= F/l, applicata nel
baricentro del rettangolo q ´
z. Dunque, la distanza tra la risultante qz
e il punto A è uguale a z/2. Per la condizione di annullamento del
momento risultante delle forze rispetto alla retta d'azione della risultante, si
può scrivere (Teorema dell'asse centrale):
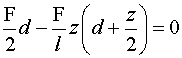
dove a q è stato sostituito il suo valore, F/l. Si ricava:
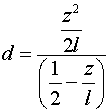
Analizziamo il segno di d: la quantità a numeratore è sempre positiva,
mentre il denominatore è positivo per 0
≤ z <
l/2,
nullo per z = l/2 e negativo per
l/2 < z
≤
l. Inoltre, per z =
0 si
ottiene d = 0, il che indica che la prima retta, quella che corrisponde a
osservatore nel punto A, è la retta a. Per z crescente tra 0 e l/2,
il numeratore cresce, mentre il denominatore decresce. Poiché il rapporto tra una
quantità crescente e una decrescente è una quantità crescente, tra z
= 0
e z = l/2, d cresce con segno positivo e la retta d'azione
della risultante si sposta, con continuità, verso sinistra. Il fatto che la
retta su cui si trova la risultante sia a sinistra del punto A non deve
sorprendere, infatti, per tutto il tratto 0
≤ z <
l/2,
si ha qz < RA. Di conseguenza,
poiché la risultante di due forze discordi è esterna alle due forze e posta dalla parte
della forza di modulo maggiore, la curva delle pressioni di trova dalla parte di
RA cioè, appunto, a sinistra del
punto A.
Nel punto B, d
assume valore infinito per l'annullarsi del denominatore e la retta d'azione
della risultante diventa la retta impropria. Anche in questo caso, il risultato
ottenuto non deve sorprendere in quanto, nel punto B, la risultante del carico
distribuito "percorso" è una forza che costituisce coppia con
RA, avendo stesso modulo,
verso opposto e diversa retta d'azione. Ebbene, per quanto visto nell'apposita
scheda,
la risultante di una coppia è una forza a modulo nullo applicata su una retta a
distanza infinita, la retta impropria.
Per z =
l/2 + e,
con e piccolo a
piacere, d è ancora infinito ma cambia segno perché cambia segno il denominatore. Fisicamente, ciò corrisponde al fatto che la risultante del carico
distribuito "percorso" dall'osservatore è diventata maggiore in modulo, anche se
solo per un infinitesimo, rispetto a
RA. Quindi, la retta si porta
a destra del baricentro del rettangolo del carico distribuito, perchè è il
carico distribuito ad essere la forza di modulo maggiore, rimanendo a
distanza infinita.
Nel tratto compreso tra B e C, il valore assoluto di
d decresce e la retta si sposta dall'infinito (con segno negativo) verso il punto il B. Infine per z
= l,
si ricava d = –
l. Dunque, l'ultima retta del fascio di rette
parallele (fascio improprio) coincide con la retta d'azione del vincolo in C.
D'altra parte, così doveva essere dal momento che, arrivato in z
= l,
l'osservatore ha "visto"
RA e tutto il carico
distribuito e, per l'equilibrio della struttura, il carico distribuito e
RA devono equilibrare la
reazione vincolare in C. Quanto detto è riassunto nella seguente tabella:
|
Tratto |
Curva delle pressioni |
|
AB
BC |
fascio di rette parallele
alla retta a, da A a +∞
fascio di rette parallele
alla retta a, da -∞ a C
|
Il fatto che il passaggio da uno all'altro fascio di rette parallele avvenga nel
punto medio della trave dipende dal valore delle reazioni vincolari, pari alla
metà della risultante del carico distribuito, ma non è un risultato
generalizzabile. Per determinare la posizione della sezione nella quale la
risultante si trova sulla retta impropria, occorre calcolare la posizione del
punto K rispetto al quale il carico distribuito assume stesso modulo e verso
opposto della risultante di tutte le altre forze che precedono K, costituendo
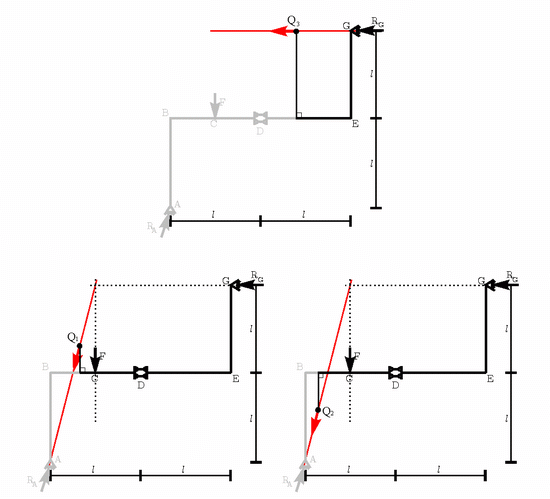
coppia con essa. A titolo di esempio, si consideri quanto si verifica nella
struttura EFG dell'esercizio di riepilogo: poiché il carico distribuito
interessa solo metà luce della trave, le reazioni vincolari assumono i valori
RE = 1/8 ql e
RG = 3/8 ql.
Pertanto, K è il punto di ascissa z2 che soddisfa la
relazione (v. figura):
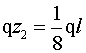
ovvero, K si trova a distanza l/8 da
RE e 7/8 l da
RG.
La trave a mensola con carico distribuito
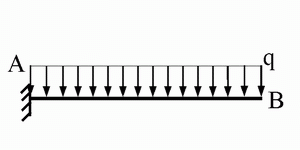
Avendo già osservato nelle
generalità che la curva delle pressioni è indipendente
dall'estremo della struttura scelto come origine di percorrenza, preoccupiamoci
di definire l'origine più conveniente per derivare la curva delle pressioni. Se
assumessimo come origine A, il punto in cui si trova il vincolo di tipo
incastro, dovremmo preventivamente calcolare le tre componenti di reazione del
vincolo per poterle comporre, trovare la retta d'azione della loro risultante e
definire così la prima retta della curva delle pressioni "vista"
dall'osservatore che si muove da A verso B. Invece, se partissimo dall'estremo
libero B, detto libero perchè in esso non è presente alcun vincolo, non dovremmo
fare altro che calcolare le successive risultanti del carico distribuito
compreso tra B e A. Dunque, la scelta più conveniente consiste proprio
nell'assume B come punto d'origine.
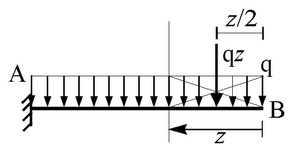
Calcoliamo ora la curva della pressioni
ricordando che la risultante della porzione di carico distribuito compresa tra
l'origine e l'ascissa z ha stessa direzione e stesso verso del carico
distribuito, ha modulo pari all'area del rettangolo di base z e altezza
q ed è applicata nel baricentro del rettangolo q
´ z. Dunque, se
l'osservatore si trova in z, la risultante del carico distribuito da lui
"visto" ha modulo qz e si trova a distanza z/2 dall'origine. Per quanto
detto, segue che:
|
Tratto |
Curva delle pressioni |
|
BA
|
fascio di rette parallele
alla retta b, comprese
tra
B e il punto medio della trave
|
N.B. Si vuol far notare che,
nella tabella riassuntiva, la trave è stata indicata come tratto BA, e non come
tratto AB. Infatti, la denominazione dei tratti deve rispettare il verso di
percorrenza prescelto, nel senso che si deve indicare per primo il nodo che
viene "visto" per primo dall'osservatore. Allo stesso modo, la dicitura
"comprese tra B e il punto medio delle trave" sta ad indicare che la retta
d'azione della risultante si sposta da B verso il punto medio quando
l'osservatore si sposta da B verso A. La convenzione di porre per primi il nodo
e la retta "visti" per primi è fondamentale per non creare ambiguità nella
definizione della curva delle pressioni. Se avessimo scelto A come punto
d'origine, avremmo dovuto scrivere:
|
Tratto |
Curva delle pressioni |
|
AB
|
fascio di rette parallele
alla retta b, comprese
tra
il punto medio della trave e B
|
Analogamente, se nell'esercizio
precedente avessimo scelto C come punto d'origine, con stessa scelta per
l'ascissa d, avremmo dovuto scrivere:
|
Tratto |
Curva delle pressioni |
|
CB
BA
|
fascio di rette parallele
alla retta a, da C a -∞
fascio di rette parallele
alla retta a, da +∞
a A
|
Il problema della definizione della curva delle pressioni si intende
risolto
correttamente solo se la corrispondenza tra verso di percorrenza
dell'osservatore e verso di traslazione della retta d'azione della risultante è
corretta. Tale corrispondenza deve risultare anche dalla figura, dove,
unitamente all'origine fissata per le z, verrà indicato anche il verso
secondo il quale risultano traslate le rette che costituiscono il fascio.
Si riportano di seguito le figure
riassuntive che devono accompagnare la tabella della curva delle pressioni, a
completamento della soluzione, per i due casi di trave a mensola e trave
appoggio-appoggio e per le due diverse scelte di origine di percorrenza.
Mensola, verso di percorrenza BA:
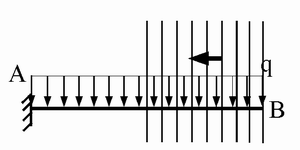
Mensola, verso di percorrenza AB:
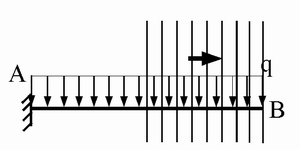
Appoggio-appoggio, verso di percorrenza AC:
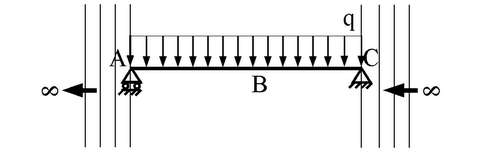
Appoggio-appoggio, verso di percorrenza CA:
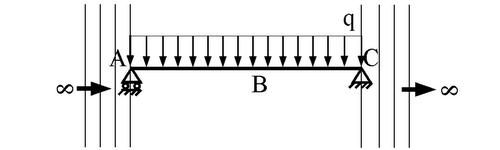
Esercizio di riepilogo
Per quanto osservato negli esempi precedenti, se su un tratto di struttura insiste un
carico distribuito la corrispondente curva delle pressioni assume la forma di:
-
un tratto parabolico, quando
la risultante delle forze che precedono il carico distribuito ha direzione diversa da quella
del carico distribuito;
-
un fascio di rette parallele, quando
la risultante delle forze
che precedono il carico distribuito o è nulla o ha stessa direzione del carico
distribuito.
Nella struttura riportata in
figura, queste due situazioni si
verificano entrambe. La curva delle pressioni tratto per tratto è riportata in
tabella, mentre le reazioni vincolari, interne ed eerne, sono riportate
direttamente sulla struttura. Si lascia al lettore il compito di verificarne
valori e rette d'azione.
|
Tratto |
Curva delle pressioni |
|
AB
BC
CD DE
EK KF
FG |
retta a
retta a
parabola tangente in
C
alla retta a e in D alla retta b
retta b
fascio di rette parallele
alla retta c, da E a +∞
fascio di rette parallele
alla retta c, da -∞
a G
retta d
|
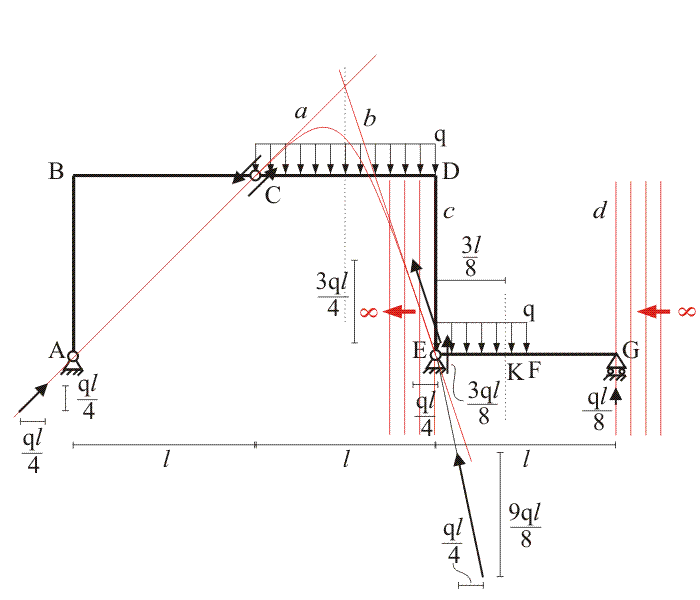
Per quanto fatto osservare al termine della discussione sulla trave a mensola,
tabella e figura riassuntive indicano che l'origine di percorrenza
dell'osservatore ideale è stata posta nel punto A. Volendo fissare l'origine
nell'estremo opposto, G, si ricaverebbe quanto segue:
|
Tratto |
Curva delle pressioni |
|
GF
FK
KE
ED
DC
CB
BA
|
retta d
fascio di rette parallele
alla retta c, da G
a -∞
fascio di rette parallele
alla retta c, da +∞
a E
retta b
parabola tangente
in D alla retta b e in C
alla retta a
retta a
retta a
|
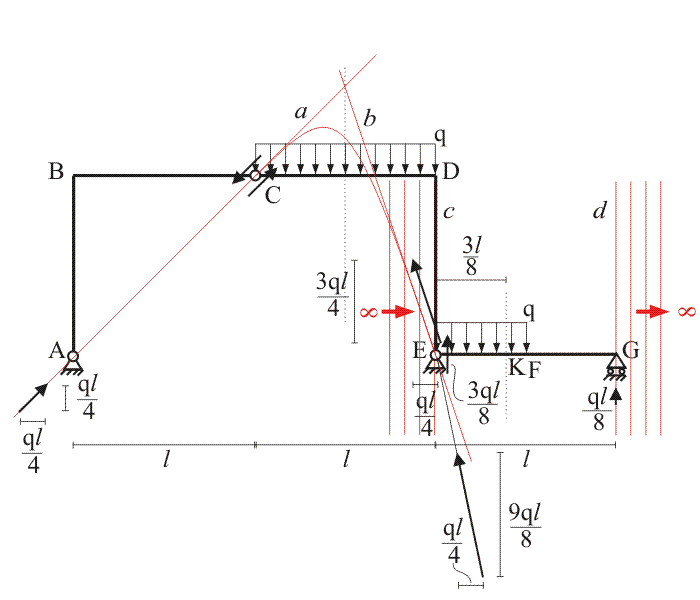
Traccia di soluzione: per semplificare la soluzione grafica dell'esercizio, può
essere conveniente operare un taglio in corrispondenza della sezione E e
studiare separatamente i due tronchi ABCDE e EFG.

Per l'equilibrio della struttura ABCDEFG, ogni suo tratto deve risultare in
equilibrio e, quindi, anche i tronchi ABCDE e EF. I vincoli posti nella
sezione di taglio (nodo E
dei due tronchi) rappresentano, in entrambi i casi, l'azione complessiva che la parte di struttura
soppressa esercitava sulla porzione in esame prima di operare il taglio. Una
volta risolte le due strutture parziali, la reazione del vincolo E nella
struttura ABCDEFG si calcola come risultante delle due reazioni vincolari
RE delle strutture parziali.
Test di verifica dell'apprendimento:
Risultante tra coppie
e forze concentrate
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con forza concentrata (es. 1)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con forza concentrata (es. 2)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con coppia concentrata
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con carico distribuito (es. 1)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con carico distribuito (es. 2)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con carico distribuito (es. 3)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con carico distribuito (es. 4)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con carico distribuito (es. 5)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con carico distribuito (es. 6)
La curva delle pressioni nelle strutture isostatiche: struttura aperta con carico
distribuito su tratto a sbalzo (es. 1)
La curva delle pressioni nelle strutture isostatiche:
struttura aperta con carico distribuito su tratto a sbalzo (es. 2)
La curva delle pressioni nelle strutture isostatiche:
struttura chiusa con forza concentrata
La curva delle pressioni nelle strutture isostatiche:
struttura chiusa con carico distribuito (es. 1)
La curva delle pressioni nelle strutture isostatiche:
struttura chiusa con carico distribuito (es. 2)
La curva delle pressioni nelle strutture isostatiche:
struttura chiusa con carico distribuito (es. 3)
La curva delle pressioni nelle strutture isostatiche:
struttura chiusa con carico distribuito (es. 4)
La curva delle pressioni nelle strutture isostatiche:
struttura chiusa con carico distribuito (es. 5)
La curva delle pressioni nelle strutture isostatiche:
struttura chiusa con carico distribuito (es. 6)